题目内容
2013年4月14日,CCTV财经频道报道了某地建筑市场存在违规使用未经淡化海砂的现象.为了研究使用淡化海砂与混凝土耐久性是否达标有关,某大学实验室随机抽取了60个样本,得到了相关数据如下表:
|
|
混凝土耐久性达标 |
混凝土耐久性不达标 |
总计 |
|
使用淡化海砂 |
25 |
|
30 |
|
使用未经淡化海砂 |
|
15 |
30 |
|
总计 |
40 |
20 |
60 |
(Ⅰ)根据表中数据,求出 ,
, 的值,利用独立性检验的方法判断,能否在犯错误的概率不超过1%的前提下,认为使用淡化海砂与混凝土耐久性是否达标有关?
的值,利用独立性检验的方法判断,能否在犯错误的概率不超过1%的前提下,认为使用淡化海砂与混凝土耐久性是否达标有关?
(Ⅱ)若用分层抽样的方法在使用淡化海砂的样本中抽取了6个,现从这6个样本中任取2个,则取出的2个样本混凝土耐久性都达标的概率是多少?
参考数据:
|
|
0.10 |
0.050 |
0.025 |
0.010 |
0.001 |
|
|
2.706 |
3.841 |
5.024 |
6.635 |
10.828 |
参考公式: 
(Ⅰ) ,能;(Ⅱ)
,能;(Ⅱ) .
.
【解析】
试题分析:(Ⅰ)由图易知 ,然后由已知数据,利用公式得
,然后由已知数据,利用公式得 通过查表可知能在犯错误的概率不超过1%的前提下,认为使用淡化海砂与混凝土耐久性是否达标有关;(Ⅱ)由图可知使用淡化海砂的样本中混凝土耐久性达标与不达标的比例为25:5,即5:1.从而知这6个样本中“混凝土耐久性达标”的为5,混凝土耐久性不达标”的为1.再计算从这6个样本中任取2个的基本事件总数,以及取出的2个样本混凝土耐久性都达标的对立事件数,再利用古典概率的公式即可得到所求概率.
通过查表可知能在犯错误的概率不超过1%的前提下,认为使用淡化海砂与混凝土耐久性是否达标有关;(Ⅱ)由图可知使用淡化海砂的样本中混凝土耐久性达标与不达标的比例为25:5,即5:1.从而知这6个样本中“混凝土耐久性达标”的为5,混凝土耐久性不达标”的为1.再计算从这6个样本中任取2个的基本事件总数,以及取出的2个样本混凝土耐久性都达标的对立事件数,再利用古典概率的公式即可得到所求概率.
试题解析:(Ⅰ) (2分)
(2分)
假设:是否使用淡化海砂与混凝土耐久性是否达标无关,由已知数据可求得:

因此,能在犯错误的概率不超过1%的前提下,认为使用淡化海砂与混凝土耐久性是否达标有关. (6分)
(Ⅱ)用分层抽样的方法在使用淡化海砂的样本中抽取了6个,其中应抽取“混凝土耐久性达标”的为 “混凝土耐久性不达标”的为1.
“混凝土耐久性不达标”的为1.
“混凝土耐久性达标”的记为 “混凝土耐久性不达标”的记为
“混凝土耐久性不达标”的记为 .
.
从这6个样本中任取2个,共有 可能,
可能,
设“取出的2个样本混凝土耐久性都达标”为事件 ,
,
它的对立事件 为“取出的2个样本至少有一个混凝土耐久性不达标”,包含(
为“取出的2个样本至少有一个混凝土耐久性不达标”,包含( ),(
),( ),
),
( ),(
),( ),(
),( )共5种可能,
)共5种可能,
所以 .
.
则取出的2个样本混凝土耐久性都达标的概率是 .
(12分)
.
(12分)
考点:1.独立性检验;2.古典概率.

2013年4月14日,CCTV财经频道报道了某地建筑市场存在违规使用未经淡化海砂的现象.为了研究使用淡化海砂与混凝土耐久性是否达标有关,某大学实验室随机抽取了60个样本,得到了相关数据如下表:
| 混凝土耐久性达标 | 混凝土耐久性不达标 | 总计 | |
| 使用淡化海砂 | 25 | 5 | 30 |
| 使用未经淡化海砂 | 15 | 15 | 30 |
| 总计 | 40 | 20 | 60 |
(2)若用分层抽样的方法在使用淡化海砂的样本中抽取了6个,现从这6个样本中任取2个,则取出的2个样本混凝土耐久性都达标的概率是多少?
参考数据:
| p(K2≥K) | 0.10 | 0.050 | 0.025 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |


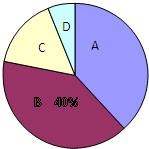 2013年4月9日至14日,西安市共有35000余名学生参加中考体育测试,为了了解九年级男生立定跳远的成绩,从某校随机抽取了50名男生的测试成绩,根据测试评分标准,将他们的得分按优秀、良好、及格、不及格(分别用A、B、C、D表示)四个等级进行统计,并绘制成下面的扇形图和统计表:
2013年4月9日至14日,西安市共有35000余名学生参加中考体育测试,为了了解九年级男生立定跳远的成绩,从某校随机抽取了50名男生的测试成绩,根据测试评分标准,将他们的得分按优秀、良好、及格、不及格(分别用A、B、C、D表示)四个等级进行统计,并绘制成下面的扇形图和统计表: