题目内容
函数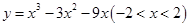 有 ( ).
有 ( ).
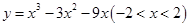 有 ( ).
有 ( ).A.极大值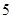 ,极小值 ,极小值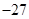 ; ; | B.极大值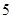 ,极小值 ,极小值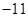 ; ; |
C.极大值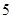 ,无极小值; ,无极小值; | D.极小值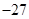 ,无极大值 ,无极大值 |
C
求出y的导函数得到x=-1,x=3(因为-2<x<2,舍去),讨论当x<-1时,y′>0;当x>-1时,y′<0,得到函数极值即可.
解:y′=3x2-6x-9=0,得x=-1,x=3,当x<-1时,y′>0;当x>-1时,y′<0,
当x=-1时,y极大值=5;x取不到3,无极小值.
故选C
解:y′=3x2-6x-9=0,得x=-1,x=3,当x<-1时,y′>0;当x>-1时,y′<0,
当x=-1时,y极大值=5;x取不到3,无极小值.
故选C

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
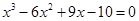 的实根个数是 ( )
的实根个数是 ( ) 在
在 处取得极值,若
处取得极值,若 ,则
,则 的最大值是____________.
的最大值是____________.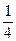
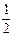
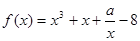
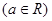 在区间
在区间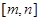 上有最大值10,则函数
上有最大值10,则函数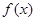 在区间
在区间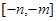 上有
上有 有极大值32.
有极大值32. 的单调区间; (2)求实数
的单调区间; (2)求实数 的值.
的值. 存在最大值M和最小值N, 则M+N的值为
存在最大值M和最小值N, 则M+N的值为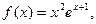
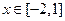 的最大值为 。
的最大值为 。