题目内容
如图所示,在棱长为2的正方体OABC—O1A1B1C1中,E、F分别为棱AB和BC上的动点,且AE=BF。
(1)求证:A1F⊥C1E;
(2)当O1B⊥EF时,求点B到平面B1EF的距离;
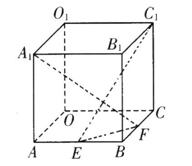 (3)在(2)的条件下,若M为棱BB1上的一点,且O1M⊥平面B1EF。试定出点M的位置,并说明理由。
(3)在(2)的条件下,若M为棱BB1上的一点,且O1M⊥平面B1EF。试定出点M的位置,并说明理由。
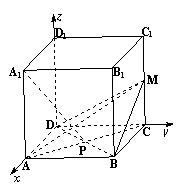
解(1)建立如图所示的空间直角坐标系O—xyz
设![]() ,则
,则![]()
∴E点为(2,t,0)F(2-t,2,0)
又A1(2,0,2),C1(0,2,2)
∴![]()
∴![]()
∴![]() 即
即![]() ……………………………5分
……………………………5分
(2)由(1)得![]()
又![]() ,∴
,∴![]() ,
,![]() ,∴E、F分别为AB、BC的中点。
,∴E、F分别为AB、BC的中点。
设点B到平面B1EF的距离为h。
由![]() 得
得![]() ………………………10分
………………………10分
(3)由M在BB1上,可设点M为(2,2,m)
则![]() ,
,![]()
由O1M⊥B1EF得![]() ,
,![]()
∴![]() ,m=1
,m=1
∴点M为BB1的中点 ……………………………15分

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
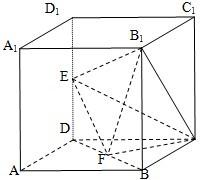 如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为DD1、DB的中点.
如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为DD1、DB的中点.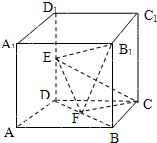 17、如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为DD1,DB的中点
17、如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为DD1,DB的中点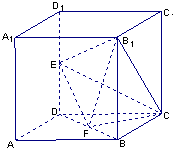 如图所示,在棱长为2的正方体中,E、F分别为DD1、BD的中点.
如图所示,在棱长为2的正方体中,E、F分别为DD1、BD的中点. 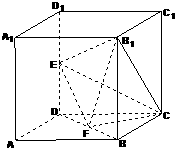 如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E、F分别为DD1、DB的中点.
如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E、F分别为DD1、DB的中点.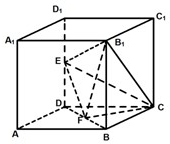 (2012•虹口区三模)如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E、F分别为DD1、DB的中点.
(2012•虹口区三模)如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E、F分别为DD1、DB的中点.