题目内容

已知f（x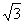）=（x>0）,数列{a_n}满足

（1）写出数列{a_n}的前5项，归纳a_n的表达式，并用数学归纳法证明；

（2）求;

（3）若b₁=,b₂= ,…,b_n=,求数列{b_n}的前n项和S_n.

解:（1）由a₁=1,a_n=得a₁=1,a₂=,a₃=,a₄=,a₅=.由此归纳得a_n=.

下面用数学归纳法证明.

①n=1时,a₁=1=,猜想成立；

②假设n=k时，a_k=，那么n=k+1时，a_k+1===.所以n=k+1时，猜想成立.

由①②，对所有n∈N^*,猜想成立，即a_n=.

（2）

=

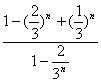==1.

（3）b_n=

=

=-.

S_n=b₁+…+b_n

=-+-+…+-

=-1.

练习册系列答案

黄冈小状元小学升学考试冲刺复习卷系列答案

毕业总复习冲刺卷系列答案

学习指导系列答案

随堂同步练习系列答案

数学奥赛天天练系列答案

数学口算每天一练系列答案

小学毕业生总复习系列答案

天天向上素质教育读本教材新解系列答案

完美学案系列答案

字词句篇与达标训练系列答案

相关题目

已知f （x）=sin （x+

），g （x）=cos （x-

），则下列命题中正确的是（　　）

A、函数y=f（x）•g（x）的最小正周期为2π

B、函数y=f（x）•g（x）是偶函数

C、函数y=f（x）+g（x）的最小值为-1

D、函数y=f（x）+g（x）的一个单调增区间是[-

已知f（x）=

．
（1）当1≤x＜2时，求g（x）；
（2）当x∈R时，求g（x）的解析式，并画出其图象；
（3）求方程x^f[g（x）]=2g[f（x）]的解．

已知f （x）=2sin（x+

．
（1）化简f （x）的解析式；
（2）若0≤θ≤π，求θ使函数f （x）为偶函数；
（3）在（2）成立的条件下，求满足f （x）=1，x∈[-π，π]的x的集合．

已知f（x）是定义在R上的奇函数，当x≥0时，f（x）=x²-kx³．（k≥0）
（Ⅰ）求g（x）的解析式；
（Ⅱ）讨论函数f（x）在区间（-∞，0）上的单调性；
（Ⅲ）若 $数学公式$ ，设g（x）是函数f（x）在区间[0，+∞）上的导函数，问是否存在实数a，满足a＞1并且使g（x）在区间 $数学公式$ 上的值域为 $数学公式$ ，若存在，求出a的值；若不存在，请说明理由．

已知f（x）是定义在R上的奇函数，当x≥0时，f（x）=x²-kx³．（k≥0）
（Ⅰ）求g（x）的解析式；
（Ⅱ）讨论函数f（x）在区间（-∞，0）上的单调性；
（Ⅲ）若

，设g（x）是函数f（x）在区间[0，+∞）上的导函数，问是否存在实数a，满足a＞1并且使g（x）在区间

上的值域为

，若存在，求出a的值；若不存在，请说明理由．