题目内容
(本题满分16分)
 已知椭圆
已知椭圆![]() 的左、右两个顶点分别为A,B,直线
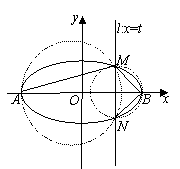
的左、右两个顶点分别为A,B,直线![]() 与椭圆相交于M,N两点,经过三点A,M,N的圆与经过三点B,M,N的圆分别记为圆C1与圆C2.
与椭圆相交于M,N两点,经过三点A,M,N的圆与经过三点B,M,N的圆分别记为圆C1与圆C2.
(1)求证:无论t如何变化,圆C1与圆C2的圆心距是定值;
(2)当t变化时,求圆C1与圆C2的面积的和S的最小值.
解:(1)易得![]() 的坐标
的坐标![]() ,
,![]() 的坐标
的坐标![]()
![]() 的坐标
的坐标![]() ,
,![]() 的坐标
的坐标![]() ,
,
线段![]() 的中点
的中点![]()
![]() ,
,
直线![]() 的斜率
的斜率
又![]() ,
, ![]() 直线
直线![]() 的斜率
的斜率![]()
![]() 直线
直线![]() 的方程
的方程![]()
![]()
![]() 的坐标为
的坐标为![]() 5分
5分
同理![]() 的坐标为
的坐标为![]()
![]()
![]() ,即无论t如何变化,为圆C1与圆C2的圆心距是定值 8分
,即无论t如何变化,为圆C1与圆C2的圆心距是定值 8分
(2)圆![]() 的半径为
的半径为![]()
![]() 圆
圆![]() 的半径为
的半径为![]()
![]() (
(![]() <
<![]() <
<![]() )
)
显然![]()
![]() 时,
时,![]() 最小,
最小,![]() 15分
15分

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目


 在
在 上的单调性;
上的单调性; ,使
,使 ,则称
,则称 的不动点,现已知该函数有且仅有一个不动点,求
的不动点,现已知该函数有且仅有一个不动点,求 的值;
的值; 在
在