题目内容
(满分16分)已知定义域为![]() 的函数
的函数![]() 同时满足以下三个条件时,称
同时满足以下三个条件时,称![]() 为“友谊函数”,
为“友谊函数”,
[1] 对任意的![]() ,总有
,总有![]() ; [2]
; [2] ![]() ;
;
[3] 若![]() ,
,![]() ,且
,且![]() ,则有
,则有![]() 成立。
成立。
请解答下列各题:
(1)若已知![]() 为“友谊函数”,求
为“友谊函数”,求![]() 的值;
的值;
(2)函数![]() 在区间
在区间![]() 上是否为“友谊函数”?并给出理由.
上是否为“友谊函数”?并给出理由.
(3)已知![]() 为“友谊函数”,假定存在
为“友谊函数”,假定存在![]() ,使得
,使得![]() 且
且![]() ,求证:
,求证:![]() .
.
解析:(1)取![]() 得
得![]() ,又由
,又由![]() ,得
,得![]()
(2)显然![]() 在
在![]() 上满足[1]
上满足[1] ![]() ;[2]
;[2] ![]() .若
.若![]() ,
,![]() ,且
,且![]() ,则有
,则有
![]()
![]()
故![]() 满足条件[1]、[2]、[3],所以
满足条件[1]、[2]、[3],所以![]() 为友谊函数.
为友谊函数.
(3)由 [3]知任给![]() 其中
其中![]() ,且有
,且有![]() ,不妨设
,不妨设![]()
则必有:![]() 所以:
所以:
![]()
所以:![]() .依题意必有
.依题意必有![]() ,
,
下面用反证法证明:假设![]() ,则有
,则有![]() 或
或![]()
(1) 若![]() ,则
,则![]() ,这与
,这与![]() 矛盾;
矛盾;
(2) 若![]() ,则
,则![]() ,这与
,这与![]() 矛盾;
矛盾;

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
 的定义域为(0,
的定义域为(0, ),且
),且 ,设点P是函数图象上的任意一点,过点P分别作直线
,设点P是函数图象上的任意一点,过点P分别作直线 和
和 轴的垂线,垂足分别为M、N.
轴的垂线,垂足分别为M、N. 的值;
的值; 是否为定值?若是,则求出该定值,若不是,请说明理由;
是否为定值?若是,则求出该定值,若不是,请说明理由;
 的离心率为
的离心率为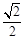 ,一条准线
,一条准线 .
. 的方程;
的方程;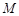 是
是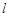 上的点,
上的点, 为椭圆
为椭圆 交于
交于 两点.
两点.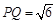 ,求圆
,求圆 在定圆上,并求该定圆的方程.
在定圆上,并求该定圆的方程. 在双曲线
在双曲线 上,圆C:
上,圆C: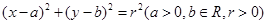 与双曲线M的一条渐近线相切于点(1,2),且圆C被x轴截得的弦长为4.(Ⅰ)求双曲线M的方程;(Ⅱ)求圆C的方程;(Ⅲ)过圆C内一定点Q(s,t)(不同于点C)任作一条直线与圆C相交于点A、B,以A、B为切点分别作圆C的切线PA、PB,求证:点P在定直线l上,并求出直线l的方程.
与双曲线M的一条渐近线相切于点(1,2),且圆C被x轴截得的弦长为4.(Ⅰ)求双曲线M的方程;(Ⅱ)求圆C的方程;(Ⅲ)过圆C内一定点Q(s,t)(不同于点C)任作一条直线与圆C相交于点A、B,以A、B为切点分别作圆C的切线PA、PB,求证:点P在定直线l上,并求出直线l的方程. 过点
过点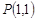 且与圆
且与圆 :
:
 关于直线
关于直线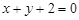 对称,作斜率为
对称,作斜率为 的直线
的直线 与圆
与圆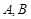 两点,且点
两点,且点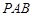 的内切圆的圆心在定直线
的内切圆的圆心在定直线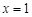 上。
上。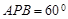 ,求△
,求△