题目内容
设倒圆锥形容器的轴截面为一个等边三角形,在此容器内注入水,并浸入半径为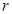 的一个实心球,使球与水面恰好相切,试求取出球后水面高为多少?
的一个实心球,使球与水面恰好相切,试求取出球后水面高为多少?
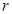 的一个实心球,使球与水面恰好相切,试求取出球后水面高为多少?
的一个实心球,使球与水面恰好相切,试求取出球后水面高为多少?

试题分析:本题实质是体积问题,我们知道题中球取出前后水的体积是不变的,通过开始时的圆锥体积减去球的体积得出水的容积,球取出后,水变成了圆锥,圆锥的高就是我们要求的水面高度.
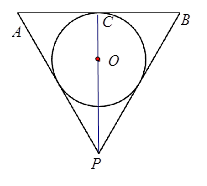
试题解析:如图为圆锥轴截面
 ,球心为
,球心为 ,可得
,可得 (3分)
(3分) (5分)
(5分)设取出球后,水面
 高为
高为 ,则
,则 (8分)
(8分)因为
 (10分)
(10分)所以
 (12分)
(12分)
练习册系列答案
相关题目
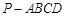 中,底面
中,底面 为矩形,
为矩形,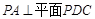 .
.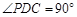 ,并指出异面直线PA与CD所成角的大小;
,并指出异面直线PA与CD所成角的大小;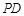 上是否存在一点
上是否存在一点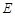 ,使得
,使得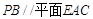 ?如果存在,求出此时三棱锥
?如果存在,求出此时三棱锥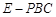 与四棱锥
与四棱锥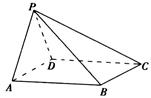
 BC,且BG⊥GC,GB=GC=2,E是BC的中点,PG=4
BC,且BG⊥GC,GB=GC=2,E是BC的中点,PG=4 ,
, ,求
,求 的值.
的值.
 平面ABE,AE=EB=BC=2,F为CE上的点.且BF
平面ABE,AE=EB=BC=2,F为CE上的点.且BF 
 平面DAE.
平面DAE. 

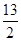
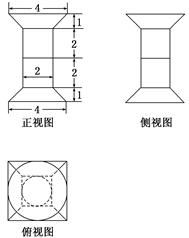
 ,比较
,比较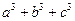 与
与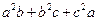 的大小。
的大小。 的各个顶点都在表面积为
的各个顶点都在表面积为 的球
的球 的球面上,其中
的球面上,其中 ,则四棱锥
,则四棱锥 的体积为( )
的体积为( )



 ,圆心角为
,圆心角为 的扇形,则此圆锥的体积为 .
的扇形,则此圆锥的体积为 .