题目内容
函数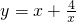
，x∈[4，6]的最小值________．
5
分析：由于函数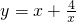在区间[0，2]单调递减，在[2，+∞）单调递增，从而可得函数在[4，6]单调递增，结合函数的单调性可求函数的最小值
解答：由于函数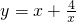在区间[0，2]单调递减，在[2，+∞）单调递增，
从而可得函数在[4，6]单调递增
所以当x=4时函数有最小值y=5
故答案为：5
点评：本题主要考查了利用函数y=x+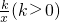
的单调性求解函数的最值，解决本题时不要错用基本不等式，因为不符合基本不等式中的等号成立条件
分析：由于函数
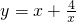在区间[0，2]单调递减，在[2，+∞）单调递增，从而可得函数在[4，6]单调递增，结合函数的单调性可求函数的最小值解答：由于函数
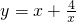在区间[0，2]单调递减，在[2，+∞）单调递增，从而可得函数在[4，6]单调递增
所以当x=4时函数有最小值y=5
故答案为：5
点评：本题主要考查了利用函数y=x+
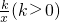的单调性求解函数的最值，解决本题时不要错用基本不等式，因为不符合基本不等式中的等号成立条件 
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
已知函数f（x）=sin（ωx+φ）（ω＞0，0＜φ＜π）的一系列对应值如下表：
（Ⅰ）求f（x）的解析式；
（Ⅱ）若在△ABC中，AC=2，BC=3，f(A)=-
，求△ABC的面积．
| x | … | -
|
0 |
|
|
|
|
… | ||||||||||
| y | … | 0 | 1 |
|
0 | -1 | 0 | … |
（Ⅱ）若在△ABC中，AC=2，BC=3，f(A)=-
| 1 |
| 2 |
，x∈[4，6]的最小值 ．