题目内容
若点P在以F1,F2为焦点的椭圆上,PF2⊥F1F2,tan∠PF1F2=
,则椭圆的离心率为______.
| 3 |
| 4 |
∵PF2⊥F1F2,tan∠PF1F2=
,
∴
=
,结合F1F2=2c为焦距,可得PF2=
c
因此,根据勾股定理可得PF1=
=
c
∴根据椭圆的定义,得椭圆的长轴2a=PF1+PF2=
c+
c=4c
由此可得椭圆的离心率为e=
=
=
=
故答案为:
| 3 |
| 4 |
∴
| PF2 |
| F1F2 |
| 3 |
| 4 |
| 3 |
| 2 |
因此,根据勾股定理可得PF1=
| PF22+F1F12 |
| 5 |
| 2 |
∴根据椭圆的定义,得椭圆的长轴2a=PF1+PF2=
| 3 |
| 2 |
| 5 |
| 2 |
由此可得椭圆的离心率为e=
| c |
| a |
| 2c |
| 2a |
| 2c |
| 4c |
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |

练习册系列答案
相关题目
 ,则椭圆的离心率为___________
,则椭圆的离心率为___________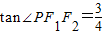 ,则椭圆的离心率为 .
,则椭圆的离心率为 .