Question

已知F₁，F₂是椭圆的两个焦点，P是椭圆上一点，且∠F₁PF₂=60°．

(1)求椭圆离心率的取值范围；

(2)求证△PF₁F₂的面积与椭圆短轴长有关．

Answer 1

思路分析：可以设椭圆方程为=1（a＞b＞0）,P(x₁,y₁)（y₁＞0）．

利用焦半径公式|PF₁|=a+ex₁,|PF₂|=a-ex₁，在△PF₁F₂中运用余弦定理，求x₁，再利用x₁∈［-a,a］，可以确定离心率e的取值范围，将x₁代入椭圆方程中求y₁，便可求出△PF₁F₂的面积．

解：设|PF₁|=m，|PF₂|=n，∠PF₂F₁=α，∠PF₁F₂=β,则α+β=120°．

(1)在△PF₁F₂中，由正弦定理,得．

∴.

∵m+n=2a，∴

∴e=．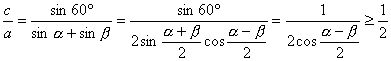

    当且仅当α=β时等号成立．故椭圆离心率的取值范围是e∈［,1)．

(2)在△PF₁F₂中，由余弦定理,得

（2c）²=m²+n²-2mncos60°

=m²+n²-mn

=（m+n）²-3mn.

∵m+n=2a，∴4c²=4a²-3mn，即mn=（a²-c²）=．

∴mnsin60°=,即△PF₁F₂的面积与椭圆短轴长有关．

方法归纳 椭圆上的一点P与两个焦点F₁，F₂构成的三角形为椭圆的焦点三角形，涉及有关焦点三角形问题，通常运用三角形的边角关系定理．解题中通过变形，使之出现|PF₁|+|PF₂|的结构，这样就可以应用椭圆的定义，从而可得到有关a,c的关系式，使问题找到解决思路．