题目内容

已知点P（1，3）为圆x2+y2+x-6y+m=0外一点，则实数m的取值范围为
(7，
37
4
)
(7，
37
4
)
．
分析：直接把点代入圆的方程的左侧，表达式大于0，并且圆的方程表示圆，即可求出m的范围．
解答：解：因为点P（1，3）为圆x2+y2+x-6y+m=0外一点，
所以1+9+1-18+m＞0，解得m＞7，
二次方程表示圆，∴1+36-4m＞0，解得m＜
37
4
，
综上：m∈(7，
37
4
)．
故答案为：(7，
37
4
)．
点评：本题考查点与圆的位置关系，注意圆的方程表示圆的条件的应用，考查计算能力．
练习册系列答案
相关题目
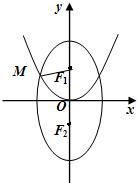精英家教网与向量、圆交汇．例5：已知F1、F2分别为椭圆C1：
y2
a2
+
x2
b2
=1(a＞b＞0)的上、下焦点，其中F1也是抛物线C2：x2=4y的焦点，点M是C1与C2在第二象限的交点，且|MF1|=
5
3
．
（1）求椭圆C1的方程；
（2）已知点P（1，3）和圆O：x2+y2=b2，过点P的动直线l与圆O相交于不同的两点A，B，在线段AB上取一点Q，满足：
AP
=-λ
PB
，
AQ
=λ
QB
，（λ≠0且λ≠±1）．问点Q是否总在某一定直线上？若在，求出这条直线，否则，说明理由．
已知点P（1，3），圆C：（x-m）2+y2=
9
2
过点A（1，-
3
2
2
），F点为抛物线y2=2px（p＞0）的焦点，直线PF与圆相切．
（1）求m的值与抛物线的方程；
（2）设点B（2，5），点 Q为抛物线上的一个动点，求
BP
•
BQ
的取值范围．
已知点P（-1，3，-4），且该点在三个坐标平面yoz平面，zox平面，xoy平面上的射影的坐标依次为（x1，y1，z1），（x2，y2，z2）和（x3，y3，z3），则（　　）
如图，已知F1、F2分别为椭圆C1：
y2
a2
+
x2
b2
=1(a＞b＞0)的上、下焦点，其中F1也是抛物线C2：x2=4y的焦点，点M是C1与C2在第二象限的交点，且|MF1|=
5
3
．
（1）求椭圆C1的方程；
（2）已知点P（1，3）和圆O：x2+y2=b2，过点P的动直线l与圆O相交于不同的两点A，B，在线段AB上取一点Q，满足：
AP
=-λ
PB
，
AQ
=λ
QB
（λ≠0且λ≠±1），
求证：点Q总在某条定直线上．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网