题目内容
已知函数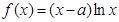 ,
,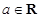 .
.
(Ⅰ)当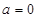 时,求函数
时,求函数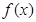 的极小值;
的极小值;
(Ⅱ)若函数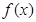 在
在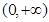 上为增函数,求
上为增函数,求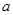 的取值范围.
的取值范围.
(Ⅰ)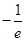 ;(Ⅱ)
;(Ⅱ)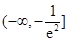
解析试题分析:(Ⅰ)先求导数,及其零点,判断导数符号变化,即可得原函数增减变化,可得其极值。(Ⅱ)函数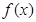 在
在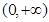 是增函数,转化为
是增函数,转化为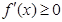 ,对
,对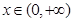 恒成立问题。即
恒成立问题。即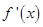 的最小值大于等于0.将问题最终转化为求
的最小值大于等于0.将问题最终转化为求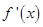 的最小值问题。仍用导数求单调性,用单调性求最值的方法求
的最小值问题。仍用导数求单调性,用单调性求最值的方法求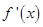 的最小值。所以需设函数
的最小值。所以需设函数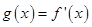 ,对函数
,对函数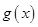 重新求导,求极值。判断导数符号变化,得
重新求导,求极值。判断导数符号变化,得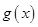 的增减区间,的最小值。
的增减区间,的最小值。
试题解析:解:(Ⅰ)定义域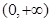 .
.
当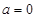 时,
时,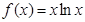 ,
,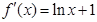 .
.
令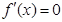 ,得
,得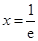 .
.
当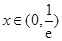 时,
时,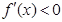 ,
,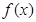 为减函数;
为减函数;
当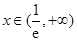 时,
时,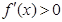 ,
,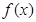 为增函数.
为增函数.
所以函数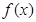 的极小值是
的极小值是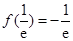 . 5分
. 5分
(Ⅱ)由已知得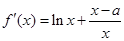 .
.
因为函数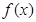 在
在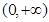 是增函数,所以
是增函数,所以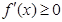 ,对
,对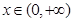 恒成立.
恒成立.
由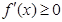 得
得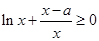 ,即
,即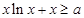 对
对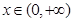 恒成立.
恒成立.
设 ,要使“
,要使“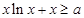 对
对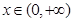 恒成立”,只要
恒成立”,只要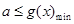 .
.
因为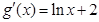 ,令
,令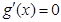 得
得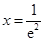 .
.
当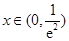 时,
时,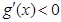 ,
,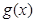 为减函数;
为减函数;
当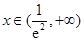 时,
时,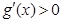 ,
,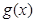 为增函数.
为增函数.
所以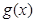 在
在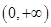 上的最小值是
上的最小值是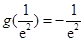 .
.
故函数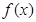 在
在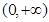 是增函数时,实数
是增函数时,实数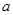 的取值范围是
的取值范围是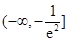 13分
13分
考点:1函数的概念和性质;2导数和利用导数研究函数性质。

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
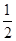 ,求证:当x∈(0,+∞)时,f(x)>1;
,求证:当x∈(0,+∞)时,f(x)>1; <e4(n∈N*)..
<e4(n∈N*)..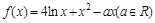 .
.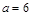 时,求函数
时,求函数 的单调区间;
的单调区间;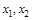 ,且
,且 ,求证:
,求证: ;
;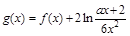 ,对于任意
,对于任意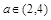 时,总存在
时,总存在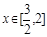 ,使
,使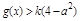 成立,求实数
成立,求实数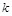 的取值范围.
的取值范围.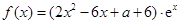 (
(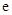 为自然对数的底数).
为自然对数的底数).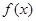 在
在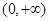 上的单调区间;
上的单调区间;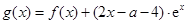 ,是否存在区间
,是否存在区间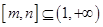 ,使得当
,使得当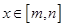 时函数
时函数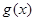 的值域为
的值域为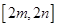 ,若存在求出
,若存在求出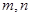 ,若不存在说明理由.
,若不存在说明理由.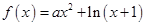 .
.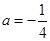 时,求函数
时,求函数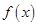 的单调区间;
的单调区间;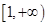 上为减函数,求实数
上为减函数,求实数 的取值范围;
的取值范围;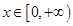 时,不等式
时,不等式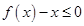 恒成立,求实数
恒成立,求实数 。
。 的极值点;
的极值点; 时,若方程
时,若方程 在
在 上有两个实数解,求实数t的取值范围;
上有两个实数解,求实数t的取值范围; 时,
时, 。
。 ,
,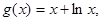 其中
其中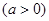
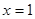 是函数
是函数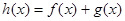 的极值点,求实数
的极值点,求实数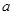 的值;
的值;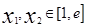 (
(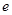 为自然对数的底数)都有
为自然对数的底数)都有 成立,求实数
成立,求实数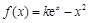 (其中
(其中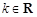 ,e是自然对数的底数).
,e是自然对数的底数).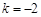 ,试判断函数
,试判断函数 在区间
在区间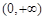 上的单调性;
上的单调性;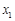 ,
,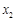 (
(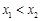 ),求k的取值范围;
),求k的取值范围;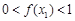 .
. 个月顾客对某种商品的需求总量
个月顾客对某种商品的需求总量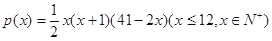 (单位:件)
(单位:件)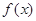 的表达式;
的表达式;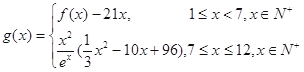 (单位:件),每件利润
(单位:件),每件利润 (单位:元),求该商场销售该商品,预计第几个月的月利润达到最大值?月利润的最大值是多少?(参考数据:
(单位:元),求该商场销售该商品,预计第几个月的月利润达到最大值?月利润的最大值是多少?(参考数据: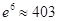 )
)