题目内容
一支人数是5的倍数且不少于1000人的游行队伍,若按每横排4人编队,最后差3人;若按每横排3人编队,最后差2人;若按每横排2人编队,最后差1人.则这只游行队伍的最少人数是( )
| A.1025 | B.1035 | C.1045 | D.1055 |
C
解析试题分析:设所求数为 ,由已知
,由已知 末尾为0或5,
末尾为0或5, 是4的倍数+1,
是4的倍数+1, 是3的倍数+1.
是3的倍数+1.
若“每横排4人编队,最后差3人 ”成立,
“每横排2人编队,最后差1人”肯定成立 不必考虑,
则  是3与4的公倍数+1,那么就是12的倍数+1
是3与4的公倍数+1,那么就是12的倍数+1
可见 末位为奇数,即为5,则
末位为奇数,即为5,则 的末位为4.
的末位为4.
可使数x满足 ,
, ;
;
要使 末尾为4,
末尾为4,
必须使  末位为2 、7 (
末位为2 、7 ( 末位都为
末位都为 ),
),
满足条件的最小 为87,所求数为1045,故选C.
为87,所求数为1045,故选C.
考点:数的整除性,推理.

练习册系列答案
相关题目
在下列区间中,函数 的零点所在的区间为( )
的零点所在的区间为( )
A.(- ,0) ,0) | B.(0, ) ) | C.( , , ) ) | D.( , , ) ) |
定义在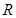 上的函数
上的函数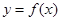 是奇函数,且满足
是奇函数,且满足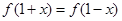 .当
.当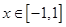 时,
时,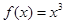 ,则
,则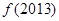 的值是( )
的值是( )
A.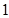 | B. | C. | D.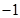 |
设f(x)=lgx+x-3,用二分法求方程lgx+x-3=0在(2,3)内近似解的过程中得f(2.25)<0,f(2.75)>0,f(2.5)<0,f(3)>0,则方程的根落在区间( )
| A.(2,2.25) | B.(2.25,2.5) |
| C.(2.5,2.75) | D.(2.75,3) |
已知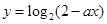 (
(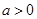 且
且 )在
)在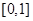 上是
上是 的减函数,则
的减函数,则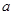 的取值范围是( )
的取值范围是( )
A.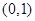 | B.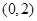 | C.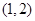 | D.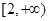 |
已知函数 是定义在
是定义在 上的偶函数,当
上的偶函数,当 时,
时, ,则函数
,则函数 的零点个数为( )
的零点个数为( )
| A.4 | B.6 | C.8 | D.10 |
已知数列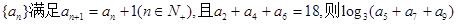 等于( )
等于( )
| A.2 | B.—2 | C.—3 | D.3 |
 是定义域R上的减函数,则函数
是定义域R上的减函数,则函数 的图象是( )
的图象是( )
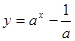
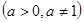 的图象可能是( )
的图象可能是( )