Question

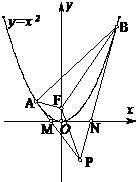（2012•安徽模拟）过抛物线y=x²上异于原点的任意两点A、B所作的两条切线交于点P，且交x轴于M、N（如图），F为抛物线的焦点．
（Ⅰ） 求点P的坐标（用A、B的横坐标x₁和x₂表示）；
（Ⅱ）求证：|FP|²=|FA|•|FB|；
（Ⅲ）设S_△OAB=λS_△PMN，试求λ的值．

Answer 1

分析：（Ⅰ）求导函数，可得切线方程，从而可求点P的坐标；
（Ⅱ）由抛物线的定义，求出|FA|、|FB|，利用两点间的距离公式，求出|FP|²，即可证得结论；
（Ⅲ）分别求出S_△OAB，S_△PMN，即可求λ的值．

解答：（Ⅰ）解：设A、B的横坐标分别为x₁和x₂，则
由y=x²可得y=2x，所以两条切线的方程分别为：
AP：y-

x

2 1

=2x1(x-x1)，BP：y-

x

2 2

=2x2(x-x2)，
联立上述两个方程解得P(

x1+x2

2

，x1x2)；          …（4分）
（Ⅱ）证明：由抛物线的定义可知：|AF|=

x

2 1

+

1

4

，|BF|=

x

2 2

+

1

4

∴|AF|•|BF|=(

x

2 1

+

1

4

)(

x

2 2

+

1

4

)=

x

2 1

x

2 2

+

1

4

(

x

2 1

+

x

2 2

)+

1

16

；
另一方面，∵F (0，

1

4

)，P(

x1+x2

2

，x1x2)，
∴|FP|2=(

x1+x2

2

)2+(x1x2-

1

4

)2=

x

2 1

x

2 2

+

1

4

(

x

2 1

+

x

2 2

)+

1

16

∴|FP|²=|FA|•|FB|；                       …（8分）
（Ⅲ）解：在（Ⅰ）中所求得的两条切线方程中分别令y=0，即求出：M(

x1

2

，0)，N(

x2

2

，0)，
∴|MN|=

1

2

|x1-x2|，
又y_P=x₁x₂，∴S△PMN=

1

4

|x1-x2|•|x1x2|；
AB的方程为：（x₁+x₂）x-y-x₁x₂=0，故点O到AB的距离为：h=

|x1x2|

1+(x1+x2)2

，
∵|AB|=

(x1-x2)2+( x 2 1 - x 2 2 )2

=|x1-x2|•

1+(x1+x2)2

，
∴S△OAB=

1

2

|AB|•h=

1

2

|x1-x2|•|x1x2|，
∴S_△OAB=2S_△PMN，
∵S_△OAB=λS_△PMN，∴λ=2．                                      …（13分）

点评：本题考查学生会利用导数求曲线上过某点切线方程的斜率，考查抛物线的定义，考查三角形面积的计算，属于中档题．