题目内容
设数列{an}是由正数组成的等比数列,公比为q,Sn是其前n项和.(1)证明
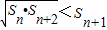 ;
;(2)设
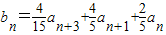 ,记数列{bn}的前n项和为Tn,试比较q2Sn和Tn的大小.
,记数列{bn}的前n项和为Tn,试比较q2Sn和Tn的大小.
【答案】分析:(1)由题设知当q=1时,Sn•Sn+2-Sn+12=na1•(n+2)a1-(n+1)2a12=-a12<0;当q≠1时,Sn•Sn+2-Sn+12= =-a12qn<0.由此可知Sn•Sn+2-Sn+12<0.所以
=-a12qn<0.由此可知Sn•Sn+2-Sn+12<0.所以 .
.
(2)方法一:由题意知Tn= ,Tn-q2Sn=
,Tn-q2Sn= ≥2,所以Tn>q2S.
≥2,所以Tn>q2S.
方法二:由题意知Tn= ,再由
,再由 ,利用均值不等式可知Tn>q2S.
,利用均值不等式可知Tn>q2S.
解答:证明:(1)由题设知a1>0,q>0.(1分)
(i)当q=1时,Sn=na1,
于是Sn•Sn+2-Sn+12=na1•(n+2)a1-(n+1)2a12=-a12<0,(3分)
(ii)当q≠1时, ,
,
于是Sn•Sn+2-Sn+12= =-a12qn<0.(7分)
=-a12qn<0.(7分)
由(i)和(ii),得Sn•Sn+2-Sn+12<0.
所以Sn•Sn+2<Sn+12, .(8分)
.(8分)
(2)方法一: ,(11分)
,(11分)
Tn= ,
,
Tn-q2Sn= ,(13分)
,(13分)
= ≥2>0,(15分)
≥2>0,(15分)
所以Tn>q2S.(16分)
方法二:Tn= ,(11分)
,(11分)
由 ,(13分)
,(13分)
因为q>0,所以
(当且仅当 ,即
,即 时取“=”号),
时取“=”号),
因为 ,
,
所以 ,即Tn>q2S.(16分)
,即Tn>q2S.(16分)
点评:本题考查数列的性质和综合应用,难度较大,解题时要认真审题,仔细解答,注意公式的合理选用.
 =-a12qn<0.由此可知Sn•Sn+2-Sn+12<0.所以
=-a12qn<0.由此可知Sn•Sn+2-Sn+12<0.所以 .
.(2)方法一:由题意知Tn=
 ,Tn-q2Sn=
,Tn-q2Sn= ≥2,所以Tn>q2S.
≥2,所以Tn>q2S.方法二:由题意知Tn=
 ,再由
,再由 ,利用均值不等式可知Tn>q2S.
,利用均值不等式可知Tn>q2S.解答:证明:(1)由题设知a1>0,q>0.(1分)
(i)当q=1时,Sn=na1,
于是Sn•Sn+2-Sn+12=na1•(n+2)a1-(n+1)2a12=-a12<0,(3分)
(ii)当q≠1时,
 ,
,于是Sn•Sn+2-Sn+12=
 =-a12qn<0.(7分)
=-a12qn<0.(7分)由(i)和(ii),得Sn•Sn+2-Sn+12<0.
所以Sn•Sn+2<Sn+12,
 .(8分)
.(8分)(2)方法一:
 ,(11分)
,(11分)Tn=
 ,
,Tn-q2Sn=
 ,(13分)
,(13分)=
 ≥2>0,(15分)
≥2>0,(15分)所以Tn>q2S.(16分)
方法二:Tn=
 ,(11分)
,(11分)由
 ,(13分)
,(13分)因为q>0,所以

(当且仅当
 ,即
,即 时取“=”号),
时取“=”号),因为
 ,
,所以
 ,即Tn>q2S.(16分)
,即Tn>q2S.(16分)点评:本题考查数列的性质和综合应用,难度较大,解题时要认真审题,仔细解答,注意公式的合理选用.

练习册系列答案
相关题目