题目内容
棱长为1的正方体ABCD-A1B1C1D1的8个顶点都在球O的表面上,E,F分别是棱AA1,DD1的中点,则直线EF被球O截得的线段长为( )
A、
| ||||
| B、1 | ||||
C、1+
| ||||
D、
|
分析:先求直径(正方体的体对角线),再求球心到EF的距离,然后解出直线EF被球O截得的线段长.
解答:解:正方体对角线为球直径,所以R2=
,在过点E、F、O的球的大圆中,
由已知得d=
,R=
,r=
=
,所以EF=2r=
.
故选D.
| 3 |
| 4 |
由已知得d=
| 1 |
| 2 |
| ||
| 2 |
|
| ||
| 2 |
| 2 |
故选D.
点评:本题考查内接体问题,考查学生空间想象能力,是基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
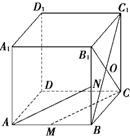 如图,在棱长为1的正方体ABCD-A1B1C1D1中,M为AB的中点,N为BB1的中点,O为平面BCC1B1的中心.
如图,在棱长为1的正方体ABCD-A1B1C1D1中,M为AB的中点,N为BB1的中点,O为平面BCC1B1的中心. 已知棱长为1的正方体容器ABCD-A1B1C1D1,在棱AB,BB1以及BC1的中点处各有一个小孔E、F、G,若此容器可以任意放置,则该容器可装水的最大容积为( )
已知棱长为1的正方体容器ABCD-A1B1C1D1,在棱AB,BB1以及BC1的中点处各有一个小孔E、F、G,若此容器可以任意放置,则该容器可装水的最大容积为( )