题目内容
(附加题 )(本小题满分14分)
已知函数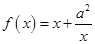 ,
,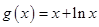 ,其中
,其中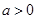 .
.
(1)若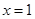 是函数
是函数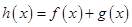 的极值点,求实数
的极值点,求实数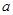 的值;
的值;
(2)若对任意的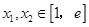 (
(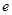 为自然对数的底数)都有
为自然对数的底数)都有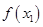 ≥
≥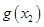 成立,求实数
成立,求实数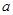 的取值范围.
的取值范围.
【答案】
(1)解法1:∵ ,其定义域为
,其定义域为 ,
,
∴ .
.
∵ 是函数
是函数 的极值点,∴
的极值点,∴ ,即
,即 .
.
∵ ,∴
,∴ .
.
经检验当 时,
时, 是函数
是函数 的极值点,
的极值点,
∴ .
.
(2)解:对任意的 都有
都有 ≥
≥ 成立等价于对任意的
成立等价于对任意的 都有
都有 ≥
≥ .
.
当
 [1,
[1, ]时,
]时, .
.
∴函数 在
在 上是增函数.
上是增函数.
∴ .
.
∵ ,且
,且 ,
, .
.
①当 且
且
 [1,
[1, ]时,
]时, ,
,
∴函数 在[1,
在[1, ]上是增函数,
]上是增函数,
∴ .
.
由 ≥
≥ ,得
,得 ≥
≥ ,
,
又 ,∴
,∴ 不合题意.
不合题意.
②当1≤ ≤
≤ 时,
时,
若1≤ <
< ,则
,则 ,
,
若 <
< ≤
≤ ,则
,则 .
.
∴函数 在
在 上是减函数,在
上是减函数,在 上是增函数.
上是增函数.
∴ .
.
由 ≥
≥ ,得
,得 ≥
≥ ,
,
又1≤ ≤
≤ ,∴
,∴ ≤
≤ ≤
≤ .
.
③当 且
且
 [1,
[1, ]时,
]时, ,
,
∴函数 在
在 上是减函数.
上是减函数.
∴ .
.
由 ≥
≥ ,得
,得 ≥
≥ ,
,
又 ,∴
,∴ .
.
综上所述, 的取值范围为
的取值范围为
【解析】略

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
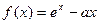 (
(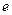 为自然对数的底数).a
为自然对数的底数).a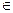 R
R 1)当a=1时,求函数
1)当a=1时,求函数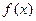 的最小值;
的最小值;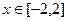 上存在极小值,求a的取值范围;
上存在极小值,求a的取值范围;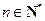 ,证明:
,证明: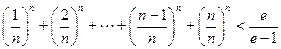 .
.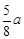 -
-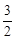 在闭区间
在闭区间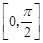 上的最大值为1?若存在,求出对应的a值;若不存在,说明理由.
上的最大值为1?若存在,求出对应的a值;若不存在,说明理由. y万件。
y万件。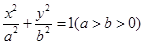 的离心率
的离心率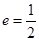 ,且原点
,且原点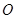 到直线
到直线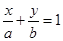 的距离为
的距离为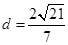 .
.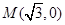 作直线与椭圆C交于
作直线与椭圆C交于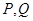 两点,求
两点,求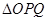 面积的最大值.
面积的最大值.