题目内容

给出下列三个类比结论．
①（ab）n=anbn与（a+b）n类比，则有（a+b）n=an+bn；
②loga（xy）=logax+logay与sin（α+β）类比，则有sin（α+β）=sinαsinβ；
③（a+b）2=a2+2ab+b2与（a+b）2类比，则有（a+b）2=a2+2a•b+b2．
其中结论正确的个数是（　　）
A．0B．1C．2D．3

根据乘方的运算法则知：（a+b）n≠an+bn，①不正确；
根据三角函数的运算法则知：sin（α+β）≠sinαsinβ，②不正确；
根据幂的运算法则知：（
a
+
b
）2=
a
2+2
a
•
b
+
b
2，③正确；
故选B．
练习册系列答案
相关题目
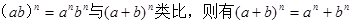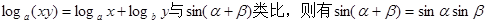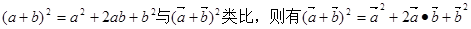8、给出下列三个类比结论．
①（ab）n=anbn与（a+b）n类比，则有（a+b）n=an+bn；
②loga（xy）=logax+logay与sin（α+β）类比，则有sin（α+β）=sinαsinβ；
③（a+b）2=a2+2ab+b2与（a+b）2类比，则有（a+b）2=a2+2a•b+b2．
其中结论正确的个数是（　　）
给出下列三个类比结论：
①（ab）n=anbn与（a+b）n类比，则有（a+b）n=an+bn；（其中a，b∈R）
②loga（xy）=logax+logay与sin（α+β）类比，则有sin（α+β）=sin αsin β；（其中x，y∈R+，α，β∈R）
③（a+b）2=a2+2ab+b2与（z1+z2）2类比，则有（z1+z2）2=z12+2z1•z2+z22．（其中a，b∈R；z1z2∈C）
其中结论正确的是
 
．

给出下列三个类比结论：

①(ab)n＝anbn与(a＋b)n类比，则有(a＋b)n＝an＋bn；

②loga(xy)＝logax＋logay与sin(α＋β)类比，则有sin(α＋β)＝sin αsin β；

③(a＋b)2＝a2＋2ab＋b2与(a＋b)2类比，则有(a＋b)2＝a2＋2a·b＋b2.

其中结论正确的个数是(　　)．

A．0        B．1         C．2          D．3

给出下列三个类比结论

①；

②；

③；

其中正确的个数是（    ）

A．0         　B．1            C．2         　D．3

 

给出下列三个类比结论．

①(ab)n＝anbn与(a＋b)n类比，则有(a＋b)n＝an＋bn；

②loga(xy)＝logax＋logay与sin(α＋β)类比，则有sin(α＋β)＝sinαsinβ；

③(a＋b)2＝a2＋2ab＋b2与(a＋b)2类比，则有(a＋b)2＝a2＋2a·b＋b2.

其中结论正确的个数是(　　)

A．0               B．1          C．2             D．3

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网