题目内容
函数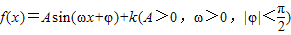
的图象如图所示，则f（x）的表达式是f（x）= ．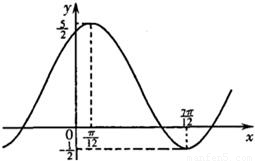
【答案】分析：由函数图象知，函数的最大值是
，最小值是
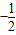，易求出A与K，又由最高点的横坐标与最低点的横坐标求出
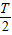，即可求出ω，再将点（
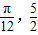）代入求出φ即可得到函数的解析式
解答：解：由图知，周期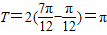
，所以ω=2．
又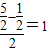
，所以k=1．
因为
，则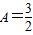
．
由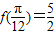
，得sin（2×
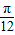+φ）=1，即得2×
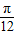+φ=
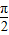得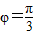
．
故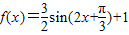
．
故答案为
点评：本题考查由f（x）=Asin（ωx+φ）+k的部分图象确定其解析式，解题的关键是从图象的几何特征得出解析式中参数的方程求出参数，求解本题难点是求初相φ的值，一般是利用最值点的坐标建立方程求之，若代入的点不是最值点，要注意其是递增区间上的点还是递减区间上的点，确定出正确的相位值，求出初相，此处易出错，要好好总结规律．
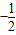，最小值是，易求出A与K，又由最高点的横坐标与最低点的横坐标求出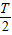，即可求出ω，再将点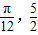（）代入求出φ即可得到函数的解析式解答：解：由图知，周期
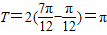，所以ω=2．又
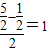，所以k=1．因为
，则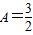．由
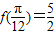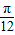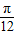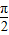，得sin（2×+φ）=1，即得2×+φ=得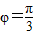．故
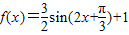．故答案为
点评：本题考查由f（x）=Asin（ωx+φ）+k的部分图象确定其解析式，解题的关键是从图象的几何特征得出解析式中参数的方程求出参数，求解本题难点是求初相φ的值，一般是利用最值点的坐标建立方程求之，若代入的点不是最值点，要注意其是递增区间上的点还是递减区间上的点，确定出正确的相位值，求出初相，此处易出错，要好好总结规律．
练习册系列答案
阅读快车系列答案
相关题目
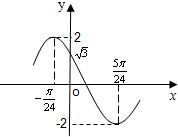已知函数f（x）=2sin（ωx+φ）（ω＞0，0＜φ＜π），且函数的图象如图所示，则点（ω，φ）的坐标是（ ）A、(2，
| ||
B、(4，
| ||
C、(2，
| ||
D、(4，
|
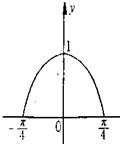已知函y=f（x）定义在[-| π |
| 4 |
| π |
| 4 |
| A、y=sinx |
| B、y=-sinx•cosx |
| C、y=sinx•cosx |
| D、y=cosx |
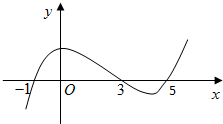函数y=f（x）导函数的图象如图所示，则下列说法正确的是：（ ）
