题目内容
圆心在直线y=x上,经过原点,且在x轴上截得弦长为2的圆的方程为( )
| A、(x-1)2+(y-1)2=2 | B、(x-1)2+(y+1)2=2 | C、(x-1)2+(y-1)2=2或(x+1)2+(y+1)2=2 | D、(x-1)2+(y+1)2=2或(x+1)2+(y-1)2=2 |
分析:根据题意画出圆的方程,使圆A满足题意中的条件,分两种情况考虑,当点A在第一象限时,根据垂径定理即可得到OC的长度,根据直线y=x上点的横纵坐标相等,得到圆心A的坐标,根据勾股定理求出OA的长度即为圆A的半径,根据求出的圆心坐标和半径写出圆的标准方程;当点A′在第三象限时,同理可得圆心坐标和半径,根据圆心坐标和半径写出圆的标准方程即可.
解答: 解:画出圆A满足题中的条件,有两个位置,
解:画出圆A满足题中的条件,有两个位置,
当圆心A在第一象限时,过A作AC⊥x轴,又|OB|=2,
根据垂径定理得到点C为弦OB的中点,则|OC|=1,由点A在直线y=x上,
得到圆心A的坐标为(1,1),且半径|OA|=
,
则圆A的标准方程为:(x-1)2+(y-1)2=2;
当圆心A′在第三象限时,过A′作A′C′⊥x轴,又|OB′|=2,
根据垂径定理得到点C′为弦OB′的中点,则|OC′|=1,由点A′在直线y=x上,
得到圆心A′的坐标为(-1,-1),且半径|OA′|=
,
则圆A′的标准方程为:(x+1)2+(y+1)2=2,
综上,满足题意的圆的方程为:(x-1)2+(y-1)2=2或(x+1)2+(y+1)2=2.
故选C
 解:画出圆A满足题中的条件,有两个位置,
解:画出圆A满足题中的条件,有两个位置,当圆心A在第一象限时,过A作AC⊥x轴,又|OB|=2,
根据垂径定理得到点C为弦OB的中点,则|OC|=1,由点A在直线y=x上,
得到圆心A的坐标为(1,1),且半径|OA|=
| 2 |
则圆A的标准方程为:(x-1)2+(y-1)2=2;
当圆心A′在第三象限时,过A′作A′C′⊥x轴,又|OB′|=2,
根据垂径定理得到点C′为弦OB′的中点,则|OC′|=1,由点A′在直线y=x上,
得到圆心A′的坐标为(-1,-1),且半径|OA′|=
| 2 |
则圆A′的标准方程为:(x+1)2+(y+1)2=2,
综上,满足题意的圆的方程为:(x-1)2+(y-1)2=2或(x+1)2+(y+1)2=2.
故选C
点评:此题考查学生灵活运用垂径定理化简求值,考查了数形结合及分类讨论的数学思想,是一道中档题.需注意的事项是应注意此题有两解,不要遗漏.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
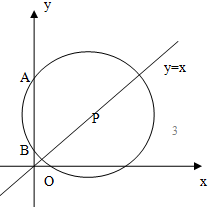 如图所示,⊙P的圆心在直线y=x上,且与直线x+2y-1=0相切,这个圆截y轴的正半轴所得的弦AB长为2,求此圆的方程.
如图所示,⊙P的圆心在直线y=x上,且与直线x+2y-1=0相切,这个圆截y轴的正半轴所得的弦AB长为2,求此圆的方程.