题目内容
已知椭圆C的左、右焦点坐标分别是(-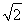 ,0),(
,0),(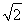 ,0),离心率是
,0),离心率是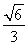 .直线y=t与椭圆C交于不同的两点M,N,以线段MN为直径作圆P,圆心为P.
.直线y=t与椭圆C交于不同的两点M,N,以线段MN为直径作圆P,圆心为P.
(1)求椭圆C的方程;
(2)若圆P与x轴相切,求圆心P的坐标;
(3)设Q(x,y)是圆P上的动点,当t变化时,求y的最大值.
【答案】
(1)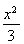 +y2=1 (2)(0,±
+y2=1 (2)(0,±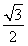 ) (3)2
) (3)2
【解析】
解:(1)因为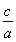 =
=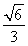 ,且c=
,且c=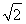 ,
,
所以a=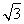 ,b=
,b=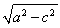 =1.
=1.
所以椭圆C的方程为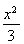 +y2=1.
+y2=1.
(2)由题意知P(0,t)(-1<t<1).
由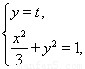
得x=±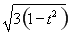 .
.
所以圆P的半径为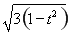 .
.
当圆P与x轴相切时,|t|=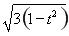 .
.
解得t=±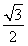 .
.
所以圆心P的坐标是(0,±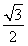 ).
).
(3)由(2)知,圆P的方程为x2+(y-t)2=3(1-t2).
因为点Q(x,y)在圆P上,
所以y=t±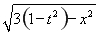 ≤t+
≤t+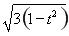 .
.
设t=cos θ,θ∈(0,π),
则t+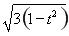 =cos θ+
=cos θ+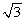 sin θ=2sin(θ+
sin θ=2sin(θ+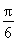 ).
).
当θ=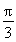 ,即t=
,即t=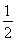 ,且x=0时,y取最大值2.
,且x=0时,y取最大值2.

练习册系列答案
相关题目
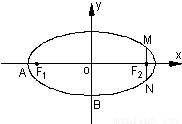
 如图,在直角坐标系xOy中,已知椭圆C:
如图,在直角坐标系xOy中,已知椭圆C:
 +
+ =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e= ,左右两个焦分别为F1、F2.过右焦点F2且与轴垂直的
,左右两个焦分别为F1、F2.过右焦点F2且与轴垂直的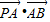 =m-4,(m∈R)试求点P的轨迹方程,使点B关于该轨迹的对称点落在椭圆C上.
=m-4,(m∈R)试求点P的轨迹方程,使点B关于该轨迹的对称点落在椭圆C上.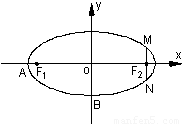
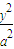 +
+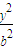 =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e=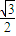 ,左右两个焦分别为F1、F2.过右焦点F2且与轴垂直的
,左右两个焦分别为F1、F2.过右焦点F2且与轴垂直的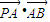 =m-4,(m∈R)试求点P的轨迹方程,使点B关于该轨迹的对称点落在椭圆C上.
=m-4,(m∈R)试求点P的轨迹方程,使点B关于该轨迹的对称点落在椭圆C上.