题目内容
三人独立破译同一份密码.已知三人各自破译出密码的概率分别为![]() 且他们是否破译出密码互不影响.
且他们是否破译出密码互不影响.
(Ⅰ)求恰有二人破译出密码的概率;
(Ⅱ)“密码被破译”与“密码未被破译”的概率哪个大?说明理由.
解:记“第i个人破译出密码”为事件Ai(i=1,2,3),依题意有
![]() 且A1,A2,A3相互独立.
且A1,A2,A3相互独立.
(Ⅰ)设“恰好二人破译出密码”为事件B,则有B=A1?A2?![]() ?A1?
?A1?![]() ?A3+
?A3+![]() ?A2?A3且A1?A2?
?A2?A3且A1?A2?![]() ,A1?
,A1?![]() ?A3,
?A3,![]() ?A2?A3彼此互斥
?A2?A3彼此互斥
于是P(B)=P(A1?A2?![]() )+P(A1?
)+P(A1?![]() ?A3)+P(
?A3)+P(![]() ?A2?A3)
?A2?A3)
=![]()
=![]() .
.
答:恰好二人破译出密码的概率为![]() .
.
(Ⅱ)设“密码被破译”为事件C,“密码未被破译”为事件D.
D=![]() ?
?![]() ?
?![]() ,且
,且![]() ,
,![]() ,
,![]() 互相独立,则有
互相独立,则有
P(D)=P(![]() )?P(
)?P(![]() )?P(
)?P(![]() )=
)=![]() =
=![]() .
.
而P(C)=1-P(D)=![]() ,故P(C)>P(D).
,故P(C)>P(D).
答:密码被破译的概率比密码未被破译的概率大.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
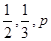 .且他们是否破译出密码互不影响.若三人中只有甲破译出密码的概率为
.且他们是否破译出密码互不影响.若三人中只有甲破译出密码的概率为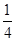 .
.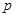 的值;
的值;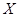 ,求
,求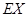 .
.