题目内容
(本小题满分14分)已知二次函数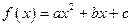 .(1)若
.(1)若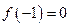 ,试判断函数
,试判断函数 零点个数;(2)若对
零点个数;(2)若对 且
且 ,
,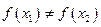 ,试证明
,试证明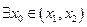 ,使
,使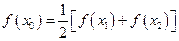 成立。(3)是否存在
成立。(3)是否存在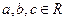 ,使
,使 同时满足以下条件①对
同时满足以下条件①对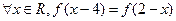 ,且
,且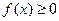 ;②对
;②对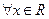 ,都有
,都有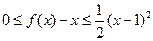 。若存在,求出
。若存在,求出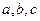 的值,若不存在,请说明理由。
的值,若不存在,请说明理由。
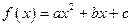 .(1)若
.(1)若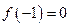 ,试判断函数
,试判断函数 零点个数;(2)若对
零点个数;(2)若对 且
且 ,
,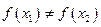 ,试证明
,试证明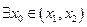 ,使
,使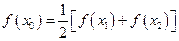 成立。(3)是否存在
成立。(3)是否存在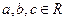 ,使
,使 同时满足以下条件①对
同时满足以下条件①对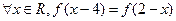 ,且
,且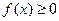 ;②对
;②对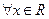 ,都有
,都有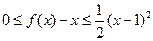 。若存在,求出
。若存在,求出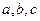 的值,若不存在,请说明理由。
的值,若不存在,请说明理由。(I) 略 (Ⅱ) 略 (III)

(1) 
 …1分
…1分
 , ……2分
, ……2分
当 时
时 ,函数
,函数 有一个零点;…3分
有一个零点;…3分
当 时,
时, ,函数
,函数 有两个零点。……4分
有两个零点。……4分
(2)令 ,则
,则
 5分
5分
 ,…6分
,…6分

 在
在 内必有一个实根。即
内必有一个实根。即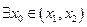 ,使
,使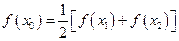 成立。…………8分
成立。…………8分
(3) 假设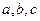 存在,由①知抛物线的对称轴为x=-1,且
存在,由①知抛物线的对称轴为x=-1,且
∴

 9分
9分
由②知对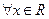 ,都有
,都有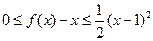
令 得
得



由 得
得 , …………12分
, …………12分
当 时,
时, ,其顶点为(-1,0)满足条件①,又
,其顶点为(-1,0)满足条件①,又
 对
对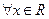 ,都有
,都有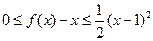 ,满足条件②。
,满足条件②。
∴存在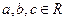 ,使
,使 同时满足条件①、②。 …………14分
同时满足条件①、②。 …………14分

 …1分
…1分 , ……2分
, ……2分当
 时
时 ,函数
,函数 有一个零点;…3分
有一个零点;…3分当
 时,
时, ,函数
,函数 有两个零点。……4分
有两个零点。……4分(2)令
 ,则
,则 5分
5分 ,…6分
,…6分
 在
在 内必有一个实根。即
内必有一个实根。即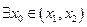 ,使
,使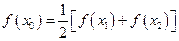 成立。…………8分
成立。…………8分(3) 假设
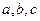 存在,由①知抛物线的对称轴为x=-1,且
存在,由①知抛物线的对称轴为x=-1,且
∴


 9分
9分由②知对
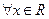 ,都有
,都有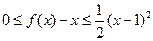
令
 得
得



由
 得
得 , …………12分
, …………12分当
 时,
时, ,其顶点为(-1,0)满足条件①,又
,其顶点为(-1,0)满足条件①,又
 对
对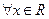 ,都有
,都有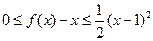 ,满足条件②。
,满足条件②。∴存在
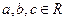 ,使
,使 同时满足条件①、②。 …………14分
同时满足条件①、②。 …………14分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,
, ,
, ,求证:
,求证: <-1;
<-1; 在(0,1)内有两个实根.
在(0,1)内有两个实根.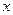 的方程
的方程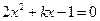
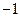 ,求另一个根及
,求另一个根及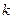 值.
值. 的零点一定位于区间
的零点一定位于区间
 是甲抛掷一枚骰子得到的点数。则方程
是甲抛掷一枚骰子得到的点数。则方程 有两个不相等的实数根的概率为
有两个不相等的实数根的概率为 B
B  C
C  D
D 