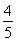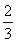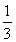题目内容
设△ABC的内角A,B,C所对的边分别为a,b,c,若bcos C+ccos B=asin A,则△ABC的形状为 ( ).
A.直角三角形 B.锐角三角形
C.钝角三角形 D.不确定
A
【解析】由正弦定理,及bcos C+ccos B=asin A,
得sin Bcos C+sin Ccos B=sin2A,即sin(B+C)=sin2A,
∴sin A=1.得A= (由于0<A<π).故△ABC是直角三角形.
(由于0<A<π).故△ABC是直角三角形.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目