题目内容
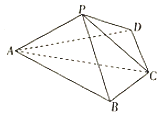
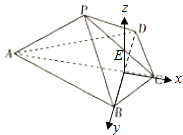
【题目】如图,四棱锥P﹣ABCD中,平面PAC⊥底面ABCD,BC=CD= ![]() AC=2,∠ACB=∠ACD=
AC=2,∠ACB=∠ACD= ![]() .
. 
(1)证明:AP⊥BD;
(2)若AP= ![]() ,AP与BC所成角的余弦值为
,AP与BC所成角的余弦值为 ![]() ,求二面角A﹣BP﹣C的余弦值..
,求二面角A﹣BP﹣C的余弦值..
【答案】
(1)证明:∵∠ACB=∠ACD= ![]() ,BC=CD.∴BD⊥AC.
,BC=CD.∴BD⊥AC.
∵平面PAC⊥底面ABCD,平面PAC∩底面ABCD=AC,
∴BD⊥平面PAC,
∴BD⊥AP
(2)解:连接BD与AC相交于点E,
∵BC=CD= ![]() ,∠ACB=∠ACD=
,∠ACB=∠ACD= ![]() .
.
则BD⊥AC,
又BD⊥平面PAC,分别以EB,EC为x,y轴,过点E与平面ABCD垂直的直线为z轴,则z轴平面APC.
可得B( ![]() ,0,0),C(0,1,0),A(0,﹣3,0),设P(0,y,
,0,0),C(0,1,0),A(0,﹣3,0),设P(0,y, ![]() ),
),
![]() =(﹣
=(﹣ ![]() ,1,0),
,1,0), ![]() =(0,y+3,
=(0,y+3, ![]() ).
).
∵AP与BC所成的余弦值为 ![]() ,
,
∴ ![]() =
= ![]() =
= 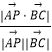 =
= ![]() ,﹣3≤y≤0,解得y=﹣1.
,﹣3≤y≤0,解得y=﹣1.
∴P(0,﹣1, ![]() ),
),
∴ ![]() =(﹣
=(﹣ ![]() ,﹣1,
,﹣1, ![]() ),
), ![]() =(
=( ![]() ,3,0),
,3,0),
设平面ABP的法向量为 ![]() =(x,y,z),
=(x,y,z),
则 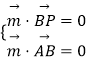 ,∴
,∴ ![]() ,
,
取 ![]() =
= ![]() .
.
∴ ![]() =
= ![]() =
= ![]() =
= ![]() .
.
∵二面角A﹣BP﹣C的平面角为钝角,
∴二面角A﹣BP﹣C的余弦值为- ![]() .
.
【解析】(1)由∠ACB=∠ACD= ![]() ,BC=CD.可得BD⊥AC.再利用面面垂直的性质可得BD⊥平面PAC,即可证明.(2)连接BD与AC相交于点E,由于BC=CD=
,BC=CD.可得BD⊥AC.再利用面面垂直的性质可得BD⊥平面PAC,即可证明.(2)连接BD与AC相交于点E,由于BC=CD= ![]() ,∠ACB=∠ACD=
,∠ACB=∠ACD= ![]() .可得BD⊥AC,又BD⊥平面PAC,分别以EB,EC为x,y轴,过点E与平面ABCD垂直的直线为z轴,则z轴平面APC.设P(0,y,
.可得BD⊥AC,又BD⊥平面PAC,分别以EB,EC为x,y轴,过点E与平面ABCD垂直的直线为z轴,则z轴平面APC.设P(0,y, ![]() ),由于AP与BC所成的余弦值为
),由于AP与BC所成的余弦值为 ![]() ,可得
,可得 ![]() =
= ![]() =
= 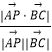 ,﹣3≤y≤0,解得y.可得P坐标,设平面ABP的法向量为
,﹣3≤y≤0,解得y.可得P坐标,设平面ABP的法向量为 ![]() =(x,y,z),利用
=(x,y,z),利用 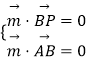 ,可得
,可得 ![]() ,同理可得平面BPC的法向量
,同理可得平面BPC的法向量 ![]() ,利用
,利用 ![]() =
= ![]() 即可得出.
即可得出.

 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案