题目内容
已知g(x)是定义在[-1,1]上的奇函数,且在区间[0,1]上满足三个条件:①对于任意的x1,x2∈[0,1],当x1<x2时,恒有g(x1)≤g(x2)成立,②g(
)=
g(x),③g(x)+g(1-x)=1.则g(
)+g(
)+g(
)=( )
| x |
| 5 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 5 |
| 1 |
| 20 |
A.
| B.
| C.
| D.
|
∵g(x)是定义在[-1,1]上的奇函数
∴g(0)=0
∵g(x)+g(1-x)=1
∴令x=1得g(1)+g(0)=1即g(1)=1
令x=
得g(
)+g(
)=1,即g(
)=
∵g(
)=
g(x)
∴令x=1得g(
)=
g(1)=
令x=
得g(
)=
g(
)=
令x=
得g(
)=
g(
)=
∵对于任意的x1,x2∈[0,1],当x1<x2时,恒有g(x1)≤g(x2)成立
∴g(
)=
∴g(
)+g(
)+g(
)=
+
+
=
故选B.
∴g(0)=0
∵g(x)+g(1-x)=1
∴令x=1得g(1)+g(0)=1即g(1)=1
令x=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵g(
| x |
| 5 |
| 1 |
| 2 |
∴令x=1得g(
| 1 |
| 5 |
| 1 |
| 2 |
| 1 |
| 2 |
令x=
| 1 |
| 2 |
| 1 |
| 10 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
令x=
| 1 |
| 5 |
| 1 |
| 25 |
| 1 |
| 2 |
| 1 |
| 5 |
| 1 |
| 4 |
∵对于任意的x1,x2∈[0,1],当x1<x2时,恒有g(x1)≤g(x2)成立
∴g(
| 1 |
| 20 |
| 1 |
| 4 |
∴g(
| 1 |
| 2 |
| 1 |
| 5 |
| 1 |
| 20 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 5 |
| 4 |
故选B.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
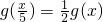 ,③g(x)+g(1-x)=1.则
,③g(x)+g(1-x)=1.则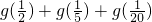 =
=



 ,③g(x)+g(1-x)=1.则
,③g(x)+g(1-x)=1.则 =( )
=( )


