题目内容
定义域为正整数集N+的函数f(x)=[log2x],其中[log2x]表示数值不超过去时log2x的最大整数.
(1)求f(3)的值;
(2)若f(x)=3,求x的取值集合;
(3)对于任意正整数n,求和:
+
+
+…+
.
(1)求f(3)的值;
(2)若f(x)=3,求x的取值集合;
(3)对于任意正整数n,求和:
| C | f(1) n |
| C | f(2) n |
| C | f(3) n |
| C | f(2n) n |
分析:(1)由log23∈(1,2)可知f(3)=[log23]=1;
(2))[log2x]=3⇒3≤log2x<4,从而可求正整数x的取值集合;
(3)依题意可知,f(2n-1)=f(2n-1+1)=…=f(2n-1+2n-1-1)=n-1(n≥1),从而可得
=
+2
+22
+…+2n-1
+1,逆用二项式定理及可求得答案.
(2))[log2x]=3⇒3≤log2x<4,从而可求正整数x的取值集合;
(3)依题意可知,f(2n-1)=f(2n-1+1)=…=f(2n-1+2n-1-1)=n-1(n≥1),从而可得
| 2n |
 |
| k=1 |
| C | f(k) n |
| C | 0 n |
| C | 1 n |
| C | 2 n |
| C | n-1 n |
解答:解:(1)∵1=log22<log23<log24=2,
∴f(3)=[log23]=1;
(2)∵[log2x]=3,
∴3≤log2x<4,
∴8≤x<16,x∈N+,
∴x的取值集合是{8,9,10,11,12,13,14,15};
(3)∵f(1)=0,
f(2)=f(3)=1,
f(4)=f(5)=f(6)=f(7)=2,
…
f(2n-1)=f(2n-1+1)=…=f(2n-1+2n-1-1)=n-1,
f(2n)=n,
∴
=
+2
+22
+…+2n-1
+1
=
+2
+22
+…+2n-1
+2n
+1-2n
=(1+2)n-2n+1
=3n-2n+1.
∴f(3)=[log23]=1;
(2)∵[log2x]=3,
∴3≤log2x<4,
∴8≤x<16,x∈N+,
∴x的取值集合是{8,9,10,11,12,13,14,15};
(3)∵f(1)=0,
f(2)=f(3)=1,
f(4)=f(5)=f(6)=f(7)=2,
…
f(2n-1)=f(2n-1+1)=…=f(2n-1+2n-1-1)=n-1,
f(2n)=n,
∴
| 2n |
 |
| k=1 |
| C | f(k) n |
| C | 0 n |
| C | 1 n |
| C | 2 n |
| C | n-1 n |
=
| C | 0 n |
| C | 1 n |
| C | 2 n |
| C | n-1 n |
| C | n n |
=(1+2)n-2n+1
=3n-2n+1.
点评:本题考查二项式定理的应用,(3)中分析得到f(2n-1)=f(2n-1+1)=…=f(2n-1+2n-1-1)=n-1是关键,也是难点,突出考查逆向思维与抽象思维能力,属于难题.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
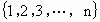 )的函数,当自变量从小到大依次取值时对应的一列函数值
)的函数,当自变量从小到大依次取值时对应的一列函数值
 )的函数,当自变量从小到大依次取值时对应的一列函数值
)的函数,当自变量从小到大依次取值时对应的一列函数值