题目内容
(本小题满分13分)对于数列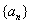 ,规定数列
,规定数列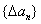 为数列
为数列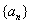 的一阶差分数列,其中
的一阶差分数列,其中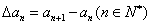 ;一般地,规定
;一般地,规定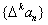 为
为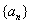 的
的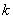 阶差分数列,其中
阶差分数列,其中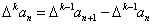 ,且
,且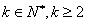 .
.
(1)已知数列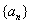 的通项公式
的通项公式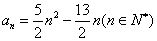 ,试证明
,试证明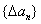 是等差数列;
是等差数列;
(2)若数列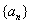 的首项
的首项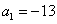 ,且满足
,且满足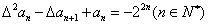 ,求数列
,求数列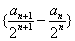 及
及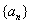 的通项公式;
的通项公式;
(3)在(2)的条件下,判断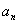 是否存在最小值,若存在求出其最小值,若不存在说明理由.
是否存在最小值,若存在求出其最小值,若不存在说明理由.
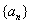 ,规定数列
,规定数列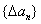 为数列
为数列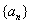 的一阶差分数列,其中
的一阶差分数列,其中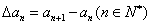 ;一般地,规定
;一般地,规定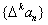 为
为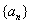 的
的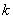 阶差分数列,其中
阶差分数列,其中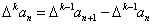 ,且
,且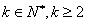 .
.(1)已知数列
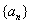 的通项公式
的通项公式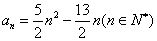 ,试证明
,试证明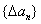 是等差数列;
是等差数列;(2)若数列
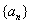 的首项
的首项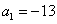 ,且满足
,且满足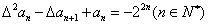 ,求数列
,求数列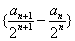 及
及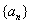 的通项公式;
的通项公式;(3)在(2)的条件下,判断
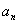 是否存在最小值,若存在求出其最小值,若不存在说明理由.
是否存在最小值,若存在求出其最小值,若不存在说明理由. ,
,  时,
时, 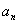 存在最小值,其最小值为-28.
存在最小值,其最小值为-28..解:(1)当 时,
时, ,则
,则
当 时 ,
时 ,
 ,则
,则

所以,数列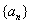 是以首项
是以首项 ,公比为
,公比为 的等比数列,从而
的等比数列,从而
(2)


当 时,
时,



又 满足,
满足,

(3)


 ①
①
而 ②
②
①-②得:



(8,9,10)20.(1)依题意: ,
,


 数列
数列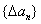 是首项为1,公差为5的等差数列.
是首项为1,公差为5的等差数列.
(2)由 得
得 ,
,
 ,
, ,
,
 ,
,  .
.
当 时,
时,


当n=1时,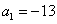 也满足上式.
也满足上式. 
(3)∵ ,令
,令 ,则
,则
 ,则当
,则当 时,函数
时,函数 单调递减; 当
单调递减; 当 时,函数
时,函数 单调递增;而
单调递增;而
∴ ,即
,即 时,
时, 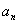 存在最小值,其最小值为-28.
存在最小值,其最小值为-28.
 时,
时, ,则
,则
当
 时 ,
时 ,
 ,则
,则

所以,数列
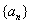 是以首项
是以首项 ,公比为
,公比为 的等比数列,从而
的等比数列,从而
(2)



当
 时,
时,



又
 满足,
满足,

(3)



 ①
① 而
 ②
②①-②得:




(8,9,10)20.(1)依题意:
 ,
,

 数列
数列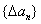 是首项为1,公差为5的等差数列.
是首项为1,公差为5的等差数列.(2)由
 得
得 ,
, ,
, ,
, ,
,  .
.当
 时,
时,


当n=1时,
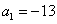 也满足上式.
也满足上式. 
(3)∵
 ,令
,令 ,则
,则 ,则当
,则当 时,函数
时,函数 单调递减; 当
单调递减; 当 时,函数
时,函数 单调递增;而
单调递增;而
∴
 ,即
,即 时,
时, 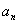 存在最小值,其最小值为-28.
存在最小值,其最小值为-28.
练习册系列答案
相关题目
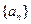 中,
中,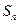 为
为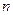 项和,
项和,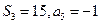 .
.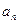 与
与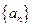 满足:
满足: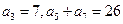 .
.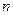 项和为
项和为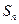 。
。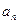 及
及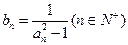 ,求数列
,求数列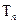 .
.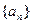 中,
中,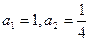 ,且
,且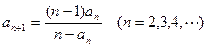 .
.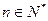 ,有
,有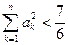 .
.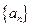 中,
中,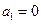 ,且对任意
,且对任意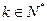 .
.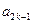 ,
,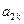 ,
,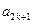 成等差数列,其公差为
成等差数列,其公差为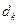 。
。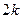 ,证明
,证明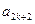 成等比数列(
成等比数列(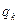 。 证明:对任意
。 证明:对任意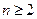 ,
,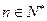 ,有
,有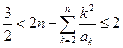
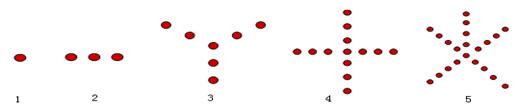
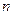 个图形中的点数
个图形中的点数 .
.
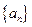 共有10项,并且其偶数项之和为30,奇数项之和为25,由此得到的结论正确的是( )
共有10项,并且其偶数项之和为30,奇数项之和为25,由此得到的结论正确的是( )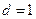
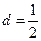
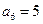
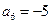

 是等差数列,且
是等差数列,且 ,则
,则 _________;
_________;