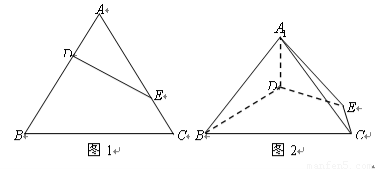
题目内容
等边三角形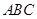 的边长为3,点
的边长为3,点 、
、 分别是边
分别是边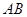 、
、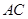 上的点,且满足
上的点,且满足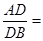
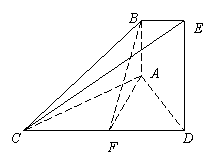
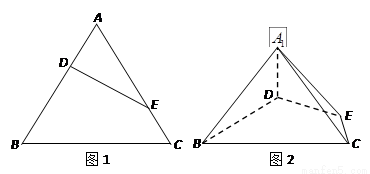
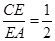 (如图1).将△
(如图1).将△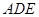 沿
沿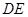 折起到△
折起到△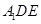 的位置,使二面角
的位置,使二面角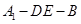 成直二面角,连结
成直二面角,连结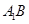 、
、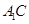 (如图2).
(如图2).
(1)求证: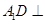 平面
平面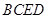 ;
;
(2)在线段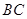 上是否存在点
上是否存在点 ,使直线
,使直线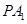 与平面
与平面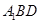 所成的角为
所成的角为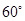 ?若存在,求出
?若存在,求出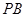 的长,若不存在,请说明理由.
的长,若不存在,请说明理由.
(1)详见解析;(2)存在,且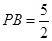 .
.
【解析】
试题分析:(1)这是一个证明题,先用利用余弦定理在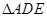 求出
求出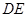 的长度,结合勾股定理证明
的长度,结合勾股定理证明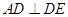 ,从而在折叠后对应地有
,从而在折叠后对应地有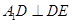 ,然后利用平面
,然后利用平面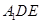
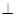 平面
平面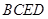 ,结合平面与平面垂直的性质定理证明
,结合平面与平面垂直的性质定理证明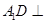 平面
平面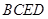 ;(2)方法1是利用(1)中的提示条件说明
;(2)方法1是利用(1)中的提示条件说明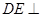 平面
平面 ,
,
然后再过点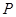 作
作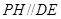 ,便可以得到
,便可以得到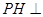 平面
平面 ,从而
,从而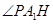 为直线
为直线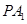 与平面
与平面 所成的角,进而围绕
所成的角,进而围绕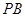 的长度进行计算;方法2是利用空间向量法,先假设点
的长度进行计算;方法2是利用空间向量法,先假设点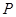 的坐标,利用(1)中的提示条件说明
的坐标,利用(1)中的提示条件说明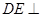 平面
平面 ,将
,将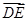 视为平面
视为平面 的一个法向量,然后利用
的一个法向量,然后利用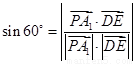 确定点
确定点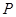 的坐标,进而计算
的坐标,进而计算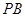 的长度.
的长度.
试题解析:证明:(1)因为等边△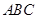 的边长为3,且
的边长为3,且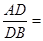
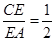 ,
,
所以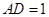 ,
,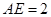 .
.
在△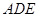 中,
中,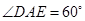 ,
,
由余弦定理得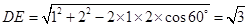 .
.
因为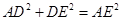 ,所以
,所以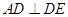 .
.
折叠后有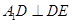 .
2分
.
2分
因为二面角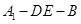 是直二面角,所以平面
是直二面角,所以平面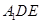
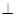 平面
平面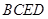 .
3分
.
3分
又平面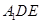
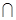 平面
平面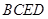
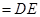 ,
,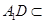 平面
平面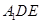 ,
,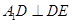 ,
,
所以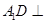 平面
平面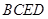 .
4分
.
4分
(2)解法1:假设在线段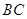 上存在点
上存在点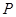 ,使直线
,使直线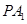 与平面
与平面 所成的角为
所成的角为 .
.
如图,作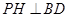 于点
于点 ,连结
,连结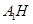 、
、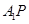 . 5分
. 5分

由(1)有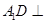 平面
平面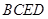 ,而
,而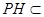 平面
平面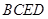 ,
,
所以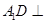
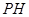 .
6分
.
6分
又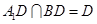 ,
,
所以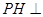 平面
平面 .
7分
.
7分
所以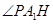 是直线
是直线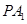 与平面
与平面 所成的角.
8分
所成的角.
8分
设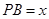
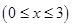 ,则
,则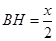 ,
,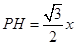 .
9分
.
9分
在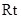 △
△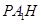 中,
中,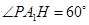 ,所以
,所以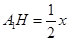 .
10分
.
10分
在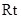 △
△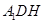 中,
中,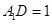 ,
,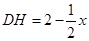 .
11分
.
11分
由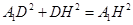 ,
,
得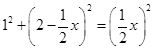 .
12分
.
12分
解得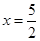 ,满足
,满足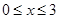 ,符合题意.
13分
,符合题意.
13分
所以在线段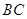 上存在点
上存在点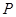 ,使直线
,使直线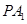 与平面
与平面 所成的角为
所成的角为 ,此时
,此时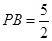 . 14分
. 14分
解法2:由(1)的证明,可知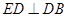 ,
,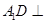 平面
平面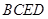 .
.
以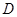 为坐标原点,以射线
为坐标原点,以射线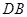 、
、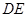 、
、 分别为
分别为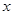 轴、
轴、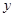 轴、
轴、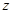 轴的正半轴,建立空间直角坐标系
轴的正半轴,建立空间直角坐标系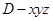 如图.
5分
如图.
5分

设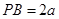
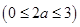 ,
,
则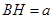 ,
,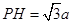 ,
,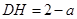 . 6分
. 6分
所以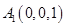 ,
,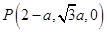 ,
,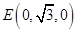 . 7分
. 7分
所以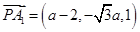 .
8分
.
8分
因为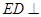 平面
平面 ,
,
所以平面 的一个法向量为
的一个法向量为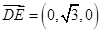 .
9分
.
9分
因为直线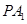 与平面
与平面 所成的角为
所成的角为 ,
,
所以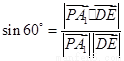 10分
10分
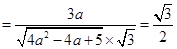 ,
11分
,
11分
解得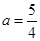 .
12分
.
12分
即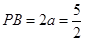 ,满足
,满足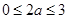 ,符合题意.
13分
,符合题意.
13分
所以在线段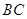 上存在点
上存在点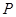 ,使直线
,使直线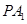 与平面
与平面 所成的角为
所成的角为 ,此时
,此时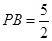 . 14分
. 14分
考点:直线与平面垂直、余弦定理、直线与平面所成的角、空间向量

 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案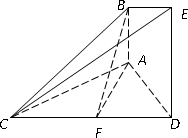
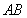
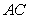

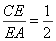
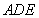
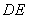
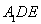
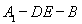
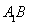
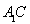
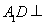
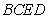
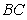
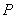
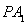
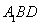
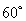
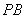
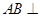 平面
平面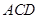 ,
,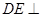 平面
平面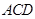 ,△
,△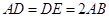 ,
, 为
为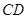 的中点.
的中点.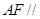 平面
平面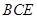 ;
;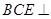 平面
平面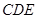 ;
;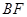 和平面
和平面