题目内容
(本题满分14分)甲、乙、丙3人投篮,投进的概率分别是![]() .
.
(Ⅰ)现3人各投篮1次,分别求3人都没有投进和3人中恰有2人投进的概率.
(Ⅱ)用ξ表示乙投篮4次的进球数,求随机变量ξ的概率分布及数学期望Eξ.
(Ⅰ) ![]() (Ⅱ)
(Ⅱ) ![]()
解析:
(Ⅰ)记"甲投篮1次投进"为事件A1 , "乙投篮1次投进"为事件A2 , "丙投篮1次投进"为事件A3, "3人都没有投进"为事件A . 则 P(A1)=![]() , P(A2)= , P(A3)= ,
, P(A2)= , P(A3)= ,
∴ P(A) = P(![]() .
.![]() .
.![]() )=P(
)=P(![]() )·P(
)·P(![]() )·P(
)·P(![]() )
)
= [1-P(A1)] ·[1-P (A2)] ·[1-P (A3)]=(1-![]() )(1-)(1-)=
)(1-)(1-)=![]()
∴3人都没有投进的概率为![]() .设“3人中恰有2人投进"为事件B
.设“3人中恰有2人投进"为事件B
![]()
=(1-![]() )×
)×![]()
![]() +
+![]()
![]()
∴3人中恰有2人投进的概率为![]() ………………7分
………………7分
(Ⅱ)解法一: 随机变量ξ的可能值有0,1,2,3, 4, ξ~ B(4, ),
∴ P(ξ=k)=![]() ()k()
()k()![]() (k=0,1,2,3, 4) ,
(k=0,1,2,3, 4) ,
ξ的概率分布为
| ξ | 0 | 1 | 2 | 3 | 4 |
| P |
|
|
|
|
|
Eξ=np = 4× = ![]() . ………………14分
. ………………14分
解法二: 随机变量ξ的可能值有0,1,2,3, 4,
![]()
![]()
![]()
![]()
![]()
ξ的概率分布为:
| ξ | 0 | 1 | 2 | 3 | 4 |
| P |
|
|
|
|
|
Eξ=0×![]() +1×
+1×![]() +2×
+2×![]() +3×
+3×![]() +4×
+4×![]() =
= ![]() .………………14分
.………………14分

练习册系列答案
相关题目

 ,第四枪瞄准了三角形
,第四枪瞄准了三角形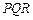 射击,第四个弹孔落在三角形
射击,第四个弹孔落在三角形 ,求第四个弹孔与前三个弹孔的距离都超过1的概率(忽略弹孔大小).
,求第四个弹孔与前三个弹孔的距离都超过1的概率(忽略弹孔大小).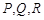 ,第四枪瞄准了三角形
,第四枪瞄准了三角形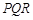 射击,第四个弹孔落在三角形
射击,第四个弹孔落在三角形