题目内容
(本题满分14分)
甲打靶射击,有4发子弹,其中有一发是空弹.
(1)求空弹出现在第一枪的概率;
(2)求空弹出现在前三枪的概率;
(3)如果把空弹换成实弹,甲前三枪在靶上留下三个两两距离分别为3,4,5的弹孔 ,第四枪瞄准了三角形
,第四枪瞄准了三角形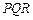 射击,第四个弹孔落在三角形
射击,第四个弹孔落在三角形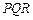 内
内 ,求第四个弹孔与前三个弹孔的距离都超过1的概率(忽略弹孔大小).
,求第四个弹孔与前三个弹孔的距离都超过1的概率(忽略弹孔大小).
解:设四发子弹编号为0(空弹),1,2,3,
(1)设第一枪出现“哑弹”的事件为A,有4个基本事件,则:(2分)

 (4分)
(4分)
法一:前三枪出现“哑弹”的事件为B,则第四枪出现“哑弹”的事件为 ,
,
那么 ,(6分)
,(6分) (9分)
(9分)
法二:前三枪共有4个基本事件{0,1,2},{0,1,3},{0,2,3},{1,2,3},满足条件的有三个,(7分)
则 (9分)
(9分)
(3)  的面积为6,(10分)
的面积为6,(10分)
分别以 为圆心、1为半径的三个扇形的面积和
为圆心、1为半径的三个扇形的面积和 ,(12分)
,(12分)
设第四个弹孔与前三个弹孔的距离都超过1的事件为C, .(14分)
.(14分)
解析

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目

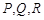 ,第四枪瞄准了三角形
,第四枪瞄准了三角形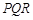 射击,第四个弹孔落在三角形
射击,第四个弹孔落在三角形