Question

【题目】在平面直角坐标系中，椭圆：经过点，且点为其一个焦点.

（1）求椭圆的方程；

（2）设椭圆与轴的两个交点为，，不在轴上的动点在直线上运动，直线，分别与椭圆交于点，，证明：直线通过一个定点，且的周长为定值.

Answer 1

【答案】（1）；（2）证明见解析.

【解析】

（1）根据题意可得a,b的方程组，解方程组即得椭圆的标准方程；（2）不妨设，.为直线上一点（），，.求出M,N的坐标，再写出直线MN的方程，再证明直线通过一个定点，求出此时的周长为定值.

（1）根据题意可得，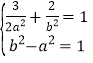

可解得，

∴椭圆的方程为.

（2）不妨设，.

为直线上一点（），，.

直线方程为，直线方程为.

点，的坐标满足方程组，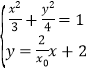

可得.

点，的坐标满足方程组，

可得，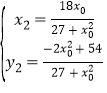

，.

直线的方程为，

即.

故直线恒过定点.

又∵，是椭圆的焦点，

∴周长.