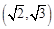题目内容
(本小题满分14分)
已知函数 ,
,
(Ⅰ)求函数 的最大值和最小正周期;
的最大值和最小正周期;
(Ⅱ)设 的内角
的内角 的对边分别
的对边分别 且
且 ,
, ,若
,若 ,求
,求 的值.
的值.
已知函数
 ,
,
(Ⅰ)求函数
 的最大值和最小正周期;
的最大值和最小正周期;(Ⅱ)设
 的内角
的内角 的对边分别
的对边分别 且
且 ,
, ,若
,若 ,求
,求 的值.
的值.(Ⅰ)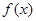 的最大值为0,最小正周期是
的最大值为0,最小正周期是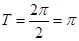 ;(Ⅱ)
;(Ⅱ)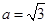 ,
, 。
。
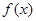 的最大值为0,最小正周期是
的最大值为0,最小正周期是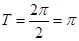 ;(Ⅱ)
;(Ⅱ)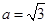 ,
, 。
。本试题主要是考查的解三角形的运用,以及三角恒等变换的综合运用。
(1)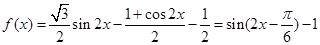 可知其周期和最值。
可知其周期和最值。
(2)因为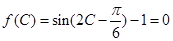 则
则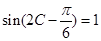 ,那么解方程得到角C的值,进而结合余弦定理得到结论。
,那么解方程得到角C的值,进而结合余弦定理得到结论。
解:(Ⅰ) ……………2分
……………2分
则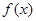 的最大值为0,最小正周期是
的最大值为0,最小正周期是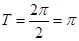 ………………4分
………………4分
(Ⅱ)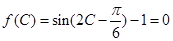 则
则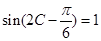
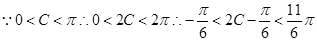
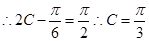 ……………………………………6分
……………………………………6分
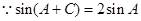 由正弦定理得
由正弦定理得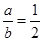 ①………………9分
①………………9分
由余弦定理得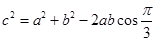
即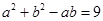 ②…………………………………12分
②…………………………………12分
由①②解得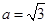 ,
, ………………………14分
………………………14分
(1)
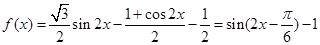 可知其周期和最值。
可知其周期和最值。(2)因为
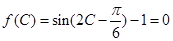 则
则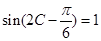 ,那么解方程得到角C的值,进而结合余弦定理得到结论。
,那么解方程得到角C的值,进而结合余弦定理得到结论。解:(Ⅰ)
 ……………2分
……………2分则
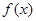 的最大值为0,最小正周期是
的最大值为0,最小正周期是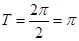 ………………4分
………………4分(Ⅱ)
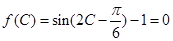 则
则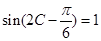
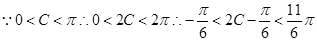
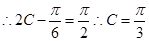 ……………………………………6分
……………………………………6分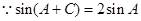 由正弦定理得
由正弦定理得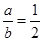 ①………………9分
①………………9分由余弦定理得
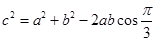
即
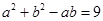 ②…………………………………12分
②…………………………………12分由①②解得
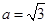 ,
, ………………………14分
………………………14分
练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
 中,内角
中,内角 的对边分别为
的对边分别为 。已知
。已知 ,
, 。(1)求
。(1)求 ;(2)若
;(2)若 ,求△
,求△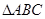 中,若
中,若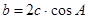 ,则这个三角形一定是( )
,则这个三角形一定是( ) 是锐角,且满足
是锐角,且满足 ,则
,则 的值为( ).
的值为( ).



 中,角
中,角 所对边分别为
所对边分别为 ,已知
,已知 .
. 的值;
的值; ,求
,求 的值.
的值. 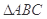 为钝角三角形,三边长分别为2,3,
为钝角三角形,三边长分别为2,3,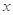 ,则
,则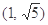



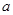 ,则
,则



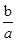 的取值范围是( )
的取值范围是( )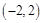 B.
B.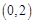 C.
C.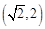 D.
D.