题目内容
如图,在四棱锥P-ABCD中,PA⊥平面ABCD, AB//CD,∠DAB=90°,PA=AD=DC=1,AB=2,M为PB的中点.

(I)证明:MC//平面PAD;
(II)求直线MC与平面PAC所成角的余弦值.

(I)证明:MC//平面PAD;
(II)求直线MC与平面PAC所成角的余弦值.
(1)根据题意,由于M为PB的中点,取PA中点E,能推理得到ME//AB,得到证明
(2)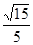
(2)
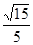
试题分析:解:
(1)
 M为PB的中点,取PA中点E,连ME,DE
M为PB的中点,取PA中点E,连ME,DE则ME//AB, 且ME=
 AB,又CD//AB, 且CD=
AB,又CD//AB, 且CD= AB,
AB,  四边形CDEM为平行四边形,
四边形CDEM为平行四边形, CM//ED, CM
CM//ED, CM 面PAD,
面PAD,  MC//平面PAD
MC//平面PAD(2)


 平面ABCD,
平面ABCD,  PA
PA BC
BC又
 ,
,  BC
BC AC
AC BC
BC 平面PAC,
平面PAC,  平面PAC
平面PAC 平面PBC, 取PC中点N,则MN//BC,
平面PBC, 取PC中点N,则MN//BC,从而MN
 平面PAC,所以
平面PAC,所以 为直线MC与平面PAC所成角,记为
为直线MC与平面PAC所成角,记为 ,
,NC=
 , MC
, MC ,
,
故直线MC与平面PAC所成角的余弦值为
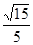
点评:主要是考查了空间中线面平行以及线面角的求解的综合运用,属于基础题。

练习册系列答案
相关题目
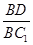 的值.
的值. 与平面
与平面 有公共点”是真命题,那么下列命题:
有公共点”是真命题,那么下列命题: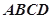 中,
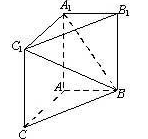
中,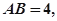 沿对角线
沿对角线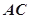 将正方形
将正方形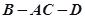 ,则点
,则点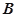 到直线
到直线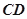 的距离为( )
的距离为( )



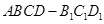 中,四边形
中,四边形 为菱形,
为菱形,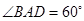 ,
,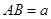 ,面
,面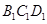 ∥面
∥面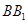 、
、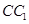 、
、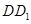 都垂直于面
都垂直于面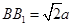 ,
, 为
为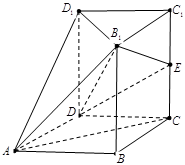
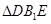 为等腰直角三角形;
为等腰直角三角形; ∥面
∥面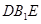 .
.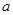 、
、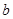 、
、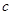 表示三条不同的直线,
表示三条不同的直线,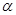 表示平面,给出下列命题:
表示平面,给出下列命题: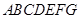 中,四边形
中,四边形 是边长为2的正方形,平面
是边长为2的正方形,平面 平面
平面 ,平面
,平面 都与平面
都与平面 、
、 、
、 都是正三角形。
都是正三角形。
 ;
; 是半圆
是半圆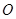 的直径,
的直径, 是半圆
是半圆 、
、 外的一个动点,
外的一个动点, 垂直于半圆
垂直于半圆 ,
, ,
, ,
, .
.
 平面
平面 ;
; 体积最大时,求二面角
体积最大时,求二面角 的余弦值.
的余弦值.