题目内容
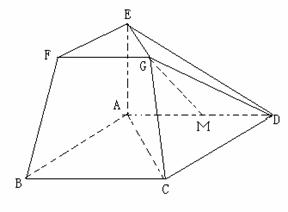
在如图所示的几何体中,四边形ABCD为平行四边形,∠ ACB=![]() ,EA⊥平面ABCD,EF∥AB,FG∥BC,EG∥AC.AB=2EF.
,EA⊥平面ABCD,EF∥AB,FG∥BC,EG∥AC.AB=2EF.
(Ⅰ)若M是线段AD的中点,求证:GM∥平面ABFE;
(Ⅱ)若AC=BC=2AE,求二面角A-BF-C的大小.
【解析】(Ⅰ)连结AF,因为EF∥AB,FG∥BC,
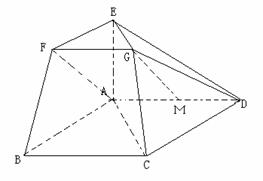
EF∩FG=F,所以平面EFG∥平面ABCD,又易证![]() ∽
∽![]() ,
,
所以![]() ,即
,即![]() ,即
,即![]() ,又M为AD
,又M为AD
的中点,所以![]() ,又因为FG∥BC∥AD,所以FG∥AM,所以四边形AMGF是平行四边形,故GM∥FA,又因为GM
,又因为FG∥BC∥AD,所以FG∥AM,所以四边形AMGF是平行四边形,故GM∥FA,又因为GM![]() 平面ABFE,FA
平面ABFE,FA![]() 平面ABFE,所以GM∥平面ABFE.
平面ABFE,所以GM∥平面ABFE.


练习册系列答案
相关题目
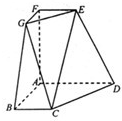 在如图所示的几何体中,四边形ABCD、ADEF、ABGF均为全等的直角梯形,且BC∥AD,AB=AD=2BC.
在如图所示的几何体中,四边形ABCD、ADEF、ABGF均为全等的直角梯形,且BC∥AD,AB=AD=2BC.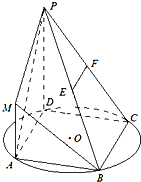 在如图所示的几何体中,平行四边形ABCD的顶点都在以AC为直径的圆O上,AD=CD=DP=a,AP=CP=
在如图所示的几何体中,平行四边形ABCD的顶点都在以AC为直径的圆O上,AD=CD=DP=a,AP=CP= (2012•朝阳区一模)在如图所示的几何体中,四边形ABCD为平行四边形,∠ABD=90°,EB⊥平面ABCD,EF∥AB,AB=2,EF=1,
(2012•朝阳区一模)在如图所示的几何体中,四边形ABCD为平行四边形,∠ABD=90°,EB⊥平面ABCD,EF∥AB,AB=2,EF=1, 在如图所示的几何体中,面CDEF为正方形,面ABCD为等腰梯形,AB∥CD,AB=2BC,∠ABC=60°,AC⊥FB.
在如图所示的几何体中,面CDEF为正方形,面ABCD为等腰梯形,AB∥CD,AB=2BC,∠ABC=60°,AC⊥FB.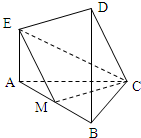 在如图所示的几何体中,EA⊥平面ABC,DB⊥平面ABC,AC⊥BC,AC=BC=BD=2AE=2,M是AB的中点.
在如图所示的几何体中,EA⊥平面ABC,DB⊥平面ABC,AC⊥BC,AC=BC=BD=2AE=2,M是AB的中点.