题目内容
已知 分别是椭圆
分别是椭圆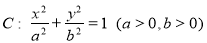 的左、右焦点,椭圆
的左、右焦点,椭圆 过点
过点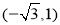 且与抛物线
且与抛物线 有一个公共的焦点.
有一个公共的焦点.
(1)求椭圆 方程;
方程;
(2)斜率为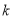 的直线
的直线 过右焦点
过右焦点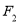 ,且与椭圆交于
,且与椭圆交于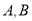 两点,求弦
两点,求弦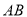 的长;
的长;
(3) 为直线
为直线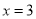 上的一点,在第(2)题的条件下,若△
上的一点,在第(2)题的条件下,若△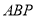 为等边三角形,求直
为等边三角形,求直
线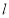 的方程.
的方程.
(1) ;(2)
;(2)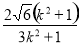 ;(3)
;(3)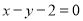 ,
,
【解析】
试题分析:(1)设椭圆的方程,若焦点明确,设椭圆的标准方程,结合条件用待定系数法求出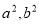 的值,若不明确,需分焦点在
的值,若不明确,需分焦点在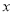 轴和
轴和 轴上两种情况讨论;(2)解决直线和椭圆的综合问题时注意:第一步:根据题意设直线方程,有的题设条件已知点,而斜率未知;有的题设条件已知斜率,点不定,可由点斜式设直线方程.第二步:联立方程:把所设直线方程与椭圆的方程联立,消去一个元,得到一个一元二次方程.第三步:求解判别式
轴上两种情况讨论;(2)解决直线和椭圆的综合问题时注意:第一步:根据题意设直线方程,有的题设条件已知点,而斜率未知;有的题设条件已知斜率,点不定,可由点斜式设直线方程.第二步:联立方程:把所设直线方程与椭圆的方程联立,消去一个元,得到一个一元二次方程.第三步:求解判别式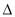 :计算一元二次方程根.第四步:写出根与系数的关系.第五步:根据题设条件求解问题中结论;(3)涉及弦长的问题时,应熟练地利用根与系数的关系,设而不求计算弦长;直线与圆锥曲线相交所得中的弦问题,就解析几何的内容之一,一般有以下三种类型:①求中点弦所在的直线方程;②求弦中点的轨迹方程问题;③弦长为定值时,弦中点的坐标问题,其解法有代点相减法、设而不求法、参数法、待定系数法及中心对称变换法.
:计算一元二次方程根.第四步:写出根与系数的关系.第五步:根据题设条件求解问题中结论;(3)涉及弦长的问题时,应熟练地利用根与系数的关系,设而不求计算弦长;直线与圆锥曲线相交所得中的弦问题,就解析几何的内容之一,一般有以下三种类型:①求中点弦所在的直线方程;②求弦中点的轨迹方程问题;③弦长为定值时,弦中点的坐标问题,其解法有代点相减法、设而不求法、参数法、待定系数法及中心对称变换法.
试题解析:(1)由题意得 
 2分
2分
又 ,
,
得 ,解得
,解得 或
或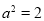 (舍去), 2分
(舍去), 2分
则 , 1分
, 1分
故椭圆方程为 . 1分
. 1分
(2)直线 的方程为
的方程为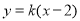 . 1分
. 1分
联立方程组
消去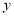 并整理得
并整理得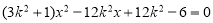 . 3分
. 3分
设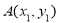 ,
, .
.
故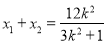 ,
, . 1分
. 1分
则
 . 2分
. 2分
(3)设 的中点为
的中点为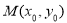 .
.
可得 , 1分
, 1分
 . 1分
. 1分
直线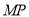 的斜率为
的斜率为 ,又
,又 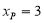 ,
,
所以 . 2分
. 2分
当△ 为正三角形时,
为正三角形时,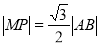 ,
,
可得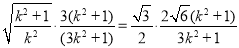 , 1分
, 1分
解得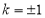 . 1分
. 1分
即直线 的方程为
的方程为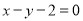 ,或
,或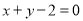 . 1分
. 1分
考点:1、求椭圆的标准方程;2、直线与圆相交求弦长;3、直线与椭圆的综合问题.

 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案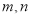 是两条不同直线,
是两条不同直线,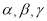 是三个不同平面,下列命题中正确的是( )
是三个不同平面,下列命题中正确的是( )

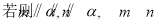
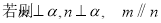
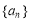 前
前 项和为
项和为 ,则下列一定成立的是
,则下列一定成立的是 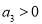 ,则
,则
 ,则
,则
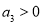 ,则
,则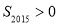
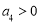 ,则
,则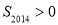
 ”组成一个四位数,则数字“
”组成一个四位数,则数字“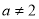 ”是“关于
”是“关于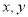 的二元一次方程组
的二元一次方程组 有唯一解”的
有唯一解”的  ,若动点
,若动点 在函数
在函数 图象上,则
图象上,则 的最小值为 .
的最小值为 . ,
,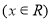 是一个以6为最小正周期的奇函数,则
是一个以6为最小正周期的奇函数,则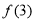 的值为( )
的值为( ) 是( )
是( )