题目内容
函数y=ax+b与指数函数y=( )x在同一直角坐标系中的图象可能是( )
)x在同一直角坐标系中的图象可能是( )A.

B.

C.

D.
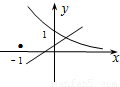
【答案】分析:先根据各个图中直线的位置确定a、b的范围,判断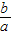 的范围,从而确定指数函数的单调性,从而得出结论.
的范围,从而确定指数函数的单调性,从而得出结论.
解答:解:对于A,由直线y=ax+b可得b>1,且 0<a<1,故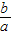 >1,
>1,
故指数函数y=(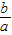 )x在定义域内是增函数,故满足条件.
)x在定义域内是增函数,故满足条件.
对于B,由直线y=ax+b可得b<-1,且 a=-1,故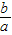 >1,
>1,
故指数函数y=( )x在定义域内是增函数,故不满足条件.
)x在定义域内是增函数,故不满足条件.
对于C,由直线y=ax+b可得b<-1,且 a>1,故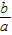 <0,故指数函数y=(
<0,故指数函数y=(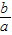 )x在无意义,故不满足条件.
)x在无意义,故不满足条件.
对于D,由直线y=ax+b可得b<0,且 a>0,故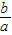 <0,故指数函数y=(
<0,故指数函数y=(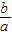 )x在无意义,故不满足条件.
)x在无意义,故不满足条件.
故选A.
点评:本题主要考查函数肚饿图象特征,注意指数函数的底数的范围,属于基础题.
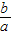 的范围,从而确定指数函数的单调性,从而得出结论.
的范围,从而确定指数函数的单调性,从而得出结论.解答:解:对于A,由直线y=ax+b可得b>1,且 0<a<1,故
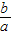 >1,
>1,故指数函数y=(
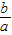 )x在定义域内是增函数,故满足条件.
)x在定义域内是增函数,故满足条件.对于B,由直线y=ax+b可得b<-1,且 a=-1,故
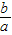 >1,
>1,故指数函数y=(
 )x在定义域内是增函数,故不满足条件.
)x在定义域内是增函数,故不满足条件.对于C,由直线y=ax+b可得b<-1,且 a>1,故
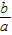 <0,故指数函数y=(
<0,故指数函数y=(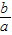 )x在无意义,故不满足条件.
)x在无意义,故不满足条件.对于D,由直线y=ax+b可得b<0,且 a>0,故
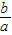 <0,故指数函数y=(
<0,故指数函数y=(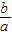 )x在无意义,故不满足条件.
)x在无意义,故不满足条件.故选A.
点评:本题主要考查函数肚饿图象特征,注意指数函数的底数的范围,属于基础题.

练习册系列答案
相关题目

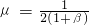 .
.