题目内容
已知函数f(x)=x-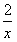 +1-alnx,a>0,
+1-alnx,a>0,
(Ⅰ)讨论f(x)的单调性;
(Ⅱ)设a=3,求f(x)在区间{1,e2}上值域,其中e=2.71828…是自然对数的底数。
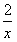 +1-alnx,a>0,
+1-alnx,a>0, (Ⅰ)讨论f(x)的单调性;
(Ⅱ)设a=3,求f(x)在区间{1,e2}上值域,其中e=2.71828…是自然对数的底数。
解:(1)由于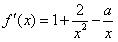 ,
,
令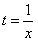 得
得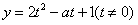 ,
,
①当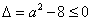 ,即
,即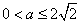 时,f(x)≥0恒成立,
时,f(x)≥0恒成立,
∴f(x)在(-∞,0)及(0,+∞)上都是增函数;
②当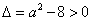 ,即
,即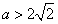 时,
时,
由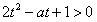 得
得 ,
,
∴ ;
;
又由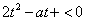 得
得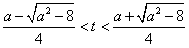 ,
,
∴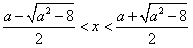 ,
,
综上,①当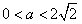 时,f(x)在(-∞,0)及(0,+∞)上都是增函数;
时,f(x)在(-∞,0)及(0,+∞)上都是增函数;
②当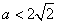 时,f(x)在
时,f(x)在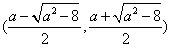 上是减函数,在
上是减函数,在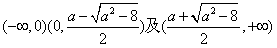 上都是增函数;
上都是增函数;
(2)当a=3时,由(1)知f(x)在[1,2]上是减函数,在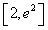 上是增函数,
上是增函数,
又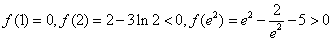 ,
,
∴函数f(x)在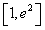 上的值域为
上的值域为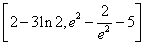 。
。
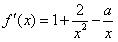 ,
,令
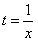 得
得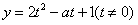 ,
,①当
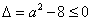 ,即
,即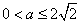 时,f(x)≥0恒成立,
时,f(x)≥0恒成立,∴f(x)在(-∞,0)及(0,+∞)上都是增函数;
②当
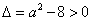 ,即
,即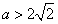 时,
时,由
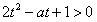 得
得 ,
,∴
 ;
;又由
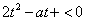 得
得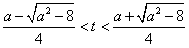 ,
,∴
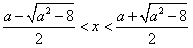 ,
,综上,①当
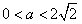 时,f(x)在(-∞,0)及(0,+∞)上都是增函数;
时,f(x)在(-∞,0)及(0,+∞)上都是增函数;②当
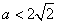 时,f(x)在
时,f(x)在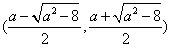 上是减函数,在
上是减函数,在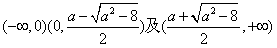 上都是增函数;
上都是增函数;(2)当a=3时,由(1)知f(x)在[1,2]上是减函数,在
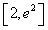 上是增函数,
上是增函数,又
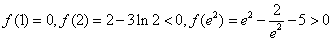 ,
,∴函数f(x)在
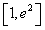 上的值域为
上的值域为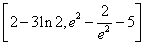 。
。
练习册系列答案
 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|