题目内容
设函数f(x)＝kx3－3x2＋1(k≥0)．
(1)求函数f(x)的单调区间；
(2)若函数f(x)的极小值大于0，求k的取值范围．
答案：
解析：
解析：
|
解：(1)当k＝0时，f(x)＝－3x2＋1， ∴f(x)的单调增区间为(－∞，0]，单调减区间为[0，＋∞)． 当k＞0时， ∴f(x)的单调增区间为(－∞，0]，[ (2)当k＝0时，函数f(x)不存在极小值． 当k＞0时，依题意f( 由条件k＞0，所以k的取值范围为(2，＋∞)． |
(x)＝3kx2－6x＝3kx(x－
)，
，＋∞)，单调减区间为[0，
＋1＞0，即k2＞4．
练习册系列答案
相关题目
，b＝e，试探究f(x)与g(x)是否存在“分界线”？若存在，求出“分界线”的方程；若不存在，请说明理由．
，b＝e，试探究f(x)与g(x)是否存在“分界线”？若存在，求出“分界线”的方程；若不存在，请说明理由．
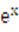－kx，.
（2）若k>0，且对于任意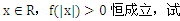
确定实数k的取值范围；[来源:学&科&网]
（
）。
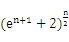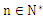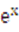－kx，.
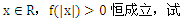确定实数k的取值范围；[来源:学&科&网]
（
）。
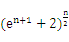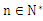－kx. 
确定实数k的取值范围；
。