题目内容
使函数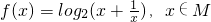 的值域为[1,2],则区间M可以是________.
的值域为[1,2],则区间M可以是________.
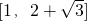 等
等分析:先由
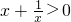 求出函数的定义域,再根据对数函数和y=
求出函数的定义域,再根据对数函数和y= 的单调性、复合函数的单调性判断原函数的单调性,再由最值求出对应的x值,根据单调性确定出可能的区间,根据要求填写一个即可.
的单调性、复合函数的单调性判断原函数的单调性,再由最值求出对应的x值,根据单调性确定出可能的区间,根据要求填写一个即可.解答:令
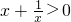 解得,x>0,故函数的定义域是(0,+∞),
解得,x>0,故函数的定义域是(0,+∞),设t=
 ,由于x>0,故t≥2,
,由于x>0,故t≥2,∵t在区间(0,1)上是减函数,在区间(1,+∞)上是增函数;且函数y=log2x在定义域上是增函数,
∴
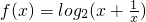 在区间(0,1)上是减函数,在区间(1,+∞)上是增函数,
在区间(0,1)上是减函数,在区间(1,+∞)上是增函数,∵
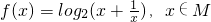 的值域为[1,2],∴当
的值域为[1,2],∴当 =2时,函数值为1;当
=2时,函数值为1;当 =4时函数值为2,
=4时函数值为2,解得:x=1;x=2
 ,
,根据函数的单调性知,区间M可以是
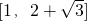 或[
或[ ,1],
,1],故答案为:
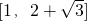 .
.点评:本题是一个开放性的题目,即根据要求选择正确答案中的一个即可,考查了对数函数的定义域、值域、单调性,对号函数的单调性和值域,复合函数的单调性问题,考查知识全面,有一定的难度.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 中,
中, ,
, .设
.设 ,记
,记 .
. 的解析式及定义域;
的解析式及定义域; ,是否存在实数
,是否存在实数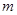 ,使函数
,使函数 的值域为
的值域为 ?若存在,求出
?若存在,求出 中,由
中,由 ,,
,, ,
,
 可得
可得

 .显然,
.显然, ,则
,则 当m>0的值域为
当m>0的值域为
 m+1=3/2,n=1/2
m+1=3/2,n=1/2 的值域为
的值域为