题目内容
已知![]() 是不为零的常数,二次函数
是不为零的常数,二次函数![]() 的定义域为R,函数
的定义域为R,函数![]() 为偶函数. 函数
为偶函数. 函数![]() 的定义域为
的定义域为![]() .
.
(1)求![]() 的值;
的值;
(2)当![]() 、
、![]() 时,求函数
时,求函数![]() 的值域;
的值域;
(3)是否存在实数![]() 、
、![]() ,使函数
,使函数![]() 的值域为
的值域为![]() ?如果存在,求出
?如果存在,求出![]() 、
、![]() 的值; 如果不存在,请说明理由.
的值; 如果不存在,请说明理由.
解:(1) ![]() , …………1
, …………1![]() 分
分
![]() , …………2分
, …………2分
由![]() 为偶函数,知
为偶函数,知![]() 恒成立,得
恒成立,得![]() ,…………3分
,…………3分
∴![]() . …………4分
. …………4分
(直接由![]() 的表达式及偶函数得出
的表达式及偶函数得出![]() ,建议不扣分;用图象平移及二次函数对称轴得出
,建议不扣分;用图象平移及二次函数对称轴得出![]() ,建议也不扣分.)
,建议也不扣分.)
(2)![]() ,对称轴为直线
,对称轴为直线![]() . …………5分
. …………5分
当![]() 、
、![]() 时,定义域为
时,定义域为![]() .
.
在![]() 上
上![]() 递增,此时函数值的集合为
递增,此时函数值的集合为![]() ,即
,即![]() ;
;
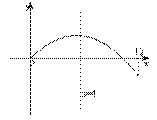 在
在![]() 上
上![]() 递减,此时函数值的集合为
递减,此时函数值的集合为![]() ,
,
即![]() (如图);
(如图);
所以,当![]() 、
、![]() 时,
时,
函数![]() 的值域为
的值域为![]() . …………8分
. …………8分
(3) 存在实数![]() 、
、![]() ,使函数
,使函数![]() 的值域为
的值域为![]() .讨论如下:
.讨论如下:
①当![]() 时,函数
时,函数![]() 在
在![]() 递增.若函数值域为
递增.若函数值域为![]() ,
,
则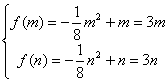 , …………9分
, …………9分
即![]() 、
、![]() 是方程
是方程![]() 的两根,而方程
的两根,而方程![]() 的两根是
的两根是![]() 、
、![]() ,所以由
,所以由![]() <
<![]() 得,
得,![]() 、
、![]() . …………10分
. …………10分
②当![]() 时,
时,
若![]() ,函数的最大值为
,函数的最大值为![]() ,则
,则![]() ,相互矛盾. …………11分
,相互矛盾. …………11分
若![]() ,函数
,函数![]() 在
在![]() 递减,函数值域为
递减,函数值域为![]() ,则
,则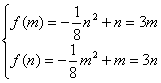 .
.
两式相减后,变形得![]() ,而
,而![]() ,
,
所以,![]() ,即
,即![]() ,
,
代入![]() 得
得![]() ,此方程无实解,此时不存在
,此方程无实解,此时不存在![]() 、
、![]() .…13分
.…13分
综上所述,存在实数![]() 、
、![]() ,使函数
,使函数![]() 的值域为
的值域为![]() . …………14分
. …………14分

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
 分别在
分别在 轴、
轴、 轴上,且满足
轴上,且满足 ,点
,点 在线段
在线段 上,且
上,且
 是不为零的常数)。设点
是不为零的常数)。设点 。
。 ,点
,点 是
是 ,
, 的面积
的面积 的最大值。
的最大值。