题目内容
设f(x),g(x)是定义在R上的恒不为零的函数,对任意x,y∈R,都有f(x)f(y)=f(x+y),g(x)+g(y)=g(x+y),若 ,且
,且 ,则数列{anbn}的前n项和为Sn为
,则数列{anbn}的前n项和为Sn为
- A.

- B.

- C.
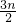
- D.
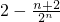
D
分析:根据f(x)f(y)=f(x+y),g(x)+g(y)=g(x+y),令x=1,y=n,分别求得数列的通项 ,bn=n,再利用错位相减法求数列的和即可.
,bn=n,再利用错位相减法求数列的和即可.
解答:∵f(x)f(y)=f(x+y),
∴令x=1,y=n可得
∴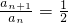
∴{an}是以 为首项,
为首项, 为公比的等比数列
为公比的等比数列
∴
∵g(x)+g(y)=g(x+y),
∴∴令x=1,y=n可得g(1)+g(n)=g(n+1)
∴bn+1-bn=g(1)=b1=1
∴数列{bn}是以1为首项,1为公差的等差数列
∴bn=n
∴数列{anbn}的前n项和为Sn=1× +2×
+2× +…+n×
+…+n×
∴ Sn=1×
Sn=1× +2×
+2× +…+(n-1)×
+…+(n-1)× +n×
+n×
两式相减可得 Sn=1×
Sn=1× +1×
+1× +1×
+1× +…+
+…+ -n×
-n×
∴Sn=2- -
-
故选D.
点评:本题考查数列的通项与求和,解题的关键是赋值,确定数列的通项,属于中档题.
分析:根据f(x)f(y)=f(x+y),g(x)+g(y)=g(x+y),令x=1,y=n,分别求得数列的通项
 ,bn=n,再利用错位相减法求数列的和即可.
,bn=n,再利用错位相减法求数列的和即可.解答:∵f(x)f(y)=f(x+y),
∴令x=1,y=n可得

∴
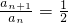
∴{an}是以
 为首项,
为首项, 为公比的等比数列
为公比的等比数列∴

∵g(x)+g(y)=g(x+y),
∴∴令x=1,y=n可得g(1)+g(n)=g(n+1)
∴bn+1-bn=g(1)=b1=1
∴数列{bn}是以1为首项,1为公差的等差数列
∴bn=n
∴数列{anbn}的前n项和为Sn=1×
 +2×
+2× +…+n×
+…+n×
∴
 Sn=1×
Sn=1× +2×
+2× +…+(n-1)×
+…+(n-1)× +n×
+n×
两式相减可得
 Sn=1×
Sn=1× +1×
+1× +1×
+1× +…+
+…+ -n×
-n×
∴Sn=2-
 -
-
故选D.
点评:本题考查数列的通项与求和,解题的关键是赋值,确定数列的通项,属于中档题.

练习册系列答案
相关题目