题目内容
(本小题满分14分)
在数列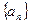 与
与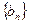 中,
中,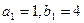 ,数列
,数列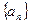 的前
的前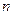 项和
项和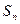 满足
满足
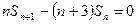 ,
,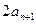 为
为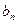 与
与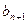 的等比中项,
的等比中项,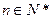 .
.
(Ⅰ)求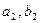 的值;
的值;
(Ⅱ)求数列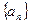 与
与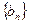 的通项公式;
的通项公式;
(Ⅲ)设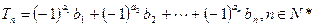 .证明
.证明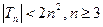 .
.
在数列
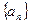 与
与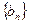 中,
中,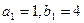 ,数列
,数列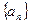 的前
的前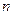 项和
项和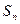 满足
满足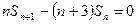 ,
,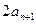 为
为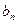 与
与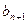 的等比中项,
的等比中项,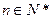 .
.(Ⅰ)求
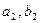 的值;
的值;(Ⅱ)求数列
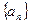 与
与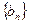 的通项公式;
的通项公式;(Ⅲ)设
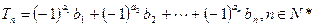 .证明
.证明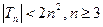 .
.(Ⅰ) ,
,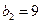
(Ⅱ)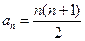 ,
,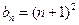
(Ⅲ)证明见解析.
 ,
,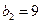
(Ⅱ)
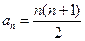 ,
,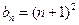
(Ⅲ)证明见解析.
本小题主要考查等差数列的概念、通项公式及前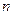 项和公式、等比数列的概念、等比中项、不等式证明、数学归纳等基础知识,考查运算能力和推理论证能力及分类讨论的思想方法.满分14分
项和公式、等比数列的概念、等比中项、不等式证明、数学归纳等基础知识,考查运算能力和推理论证能力及分类讨论的思想方法.满分14分


(Ⅰ)解:由题设有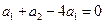 ,
,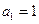 ,解得
,解得 .由题设又有
.由题设又有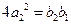 ,
,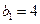 ,解得
,解得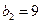 .
.
(Ⅱ)解法一:由题设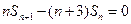 ,
,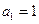 ,
,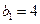 ,及
,及 ,
,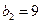 ,进一步可得
,进一步可得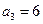 ,
,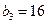 ,
,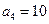 ,
,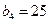 ,猜想
,猜想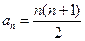 ,
,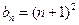 ,
,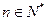 .
.
先证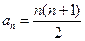 ,
,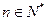 .
.
当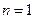 时,
时,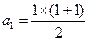 ,等式成立.当
,等式成立.当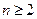 时用数学归纳法证明如下:
时用数学归纳法证明如下:
(1当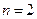 时,
时,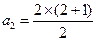 ,等式成立.
,等式成立.
(2)假设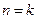 时等式成立,即
时等式成立,即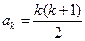 ,
,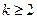 .
.
由题设,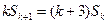
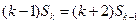
①的两边分别减去②的两边,整理得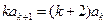 ,从而
,从而
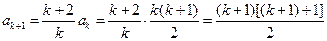 .
.
这就是说,当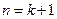 时等式也成立.根据(1)和(2)可知,等式
时等式也成立.根据(1)和(2)可知,等式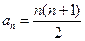 对任何的
对任何的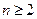 成立.
成立.
综上所述,等式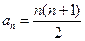 对任何的
对任何的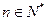 都成立
都成立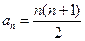
再用数学归纳法证明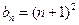 ,
,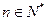 .
.
(1)当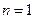 时,
时,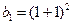 ,等式成立.
,等式成立.
(2)假设当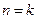 时等式成立,即
时等式成立,即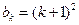 ,那么
,那么
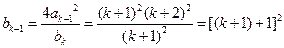 .
.
这就是说,当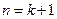 时等式也成立.根据(1)和(2)可知,等式
时等式也成立.根据(1)和(2)可知,等式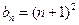 对任何的
对任何的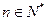 都成立.
都成立.
解法二:由题设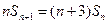
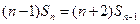
①的两边分别减去②的两边,整理得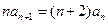 ,
,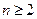 .所以
.所以
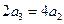 ,
,
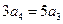 ,
,
……
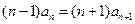 ,
,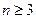 .
.
将以上各式左右两端分别相乘,得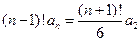 ,
,
由(Ⅰ)并化简得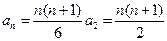 ,
,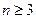 .
.
止式对 也成立.
也成立.
由题设有 ,所以
,所以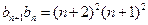 ,即
,即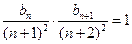 ,
,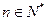 .
.
令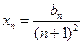 ,则
,则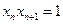 ,即
,即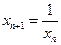 .由
.由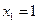 得
得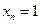 ,
,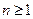 .所以
.所以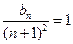 ,即
,即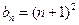 ,
,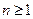 .
.
解法三:由题设有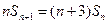 ,
,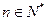 ,所以
,所以
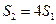 ,
,
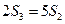 ,
,
……
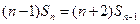 ,
,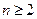 .
.
将以上各式左右两端分别相乘,得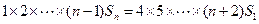 ,化简得
,化简得
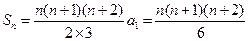 ,
,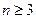 .
.
由(Ⅰ),上式对 也成立.所以
也成立.所以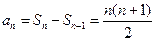 ,
,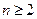 .
.
上式对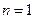 时也成立.
时也成立.
以下同解法二,可得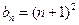 ,
,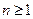 .
.
(Ⅲ)证明: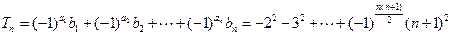 .
.
当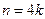 ,
,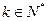 时,
时,
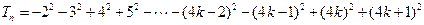 .
.
注意到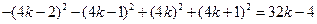 ,故
,故
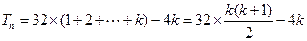
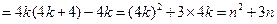 .
.
当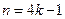 ,
,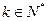 时,
时,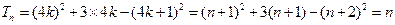
当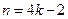 ,
,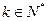 时,
时,
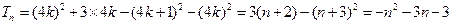 .
.
当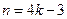 ,
,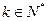 时,
时,
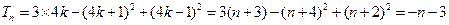 .
.
所以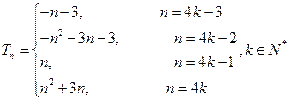 .
.
从而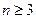 时,有
时,有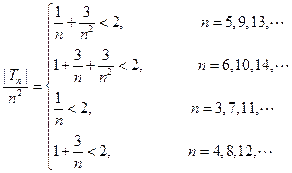
总之,当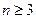 时有
时有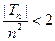 ,即
,即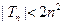 .
.
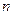 项和公式、等比数列的概念、等比中项、不等式证明、数学归纳等基础知识,考查运算能力和推理论证能力及分类讨论的思想方法.满分14分
项和公式、等比数列的概念、等比中项、不等式证明、数学归纳等基础知识,考查运算能力和推理论证能力及分类讨论的思想方法.满分14分

(Ⅰ)解:由题设有
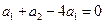 ,
,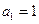 ,解得
,解得 .由题设又有
.由题设又有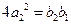 ,
,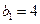 ,解得
,解得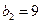 .
.(Ⅱ)解法一:由题设
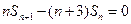 ,
,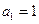 ,
,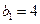 ,及
,及 ,
,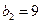 ,进一步可得
,进一步可得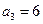 ,
,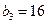 ,
,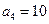 ,
,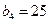 ,猜想
,猜想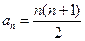 ,
,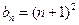 ,
,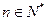 .
.先证
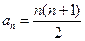 ,
,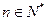 .
.当
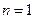 时,
时,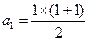 ,等式成立.当
,等式成立.当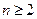 时用数学归纳法证明如下:
时用数学归纳法证明如下:(1当
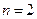 时,
时,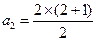 ,等式成立.
,等式成立.(2)假设
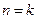 时等式成立,即
时等式成立,即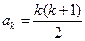 ,
,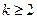 .
.由题设,
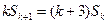
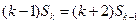
①的两边分别减去②的两边,整理得
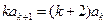 ,从而
,从而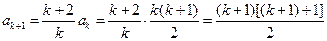 .
.这就是说,当
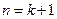 时等式也成立.根据(1)和(2)可知,等式
时等式也成立.根据(1)和(2)可知,等式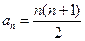 对任何的
对任何的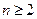 成立.
成立.综上所述,等式
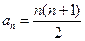 对任何的
对任何的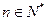 都成立
都成立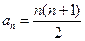
再用数学归纳法证明
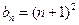 ,
,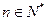 .
.(1)当
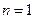 时,
时,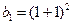 ,等式成立.
,等式成立.(2)假设当
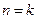 时等式成立,即
时等式成立,即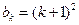 ,那么
,那么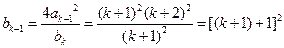 .
.这就是说,当
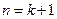 时等式也成立.根据(1)和(2)可知,等式
时等式也成立.根据(1)和(2)可知,等式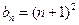 对任何的
对任何的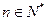 都成立.
都成立.解法二:由题设
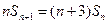
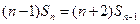
①的两边分别减去②的两边,整理得
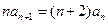 ,
,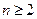 .所以
.所以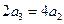 ,
,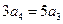 ,
,……
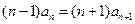 ,
,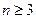 .
.将以上各式左右两端分别相乘,得
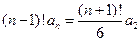 ,
,由(Ⅰ)并化简得
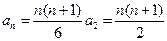 ,
,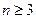 .
.止式对
 也成立.
也成立.由题设有
 ,所以
,所以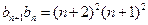 ,即
,即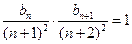 ,
,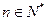 .
.令
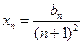 ,则
,则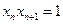 ,即
,即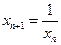 .由
.由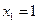 得
得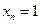 ,
,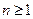 .所以
.所以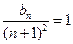 ,即
,即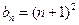 ,
,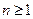 .
.解法三:由题设有
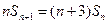 ,
,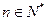 ,所以
,所以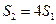 ,
,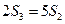 ,
,……
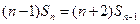 ,
,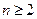 .
.将以上各式左右两端分别相乘,得
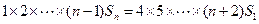 ,化简得
,化简得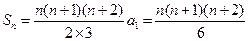 ,
,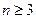 .
.由(Ⅰ),上式对
 也成立.所以
也成立.所以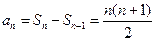 ,
,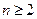 .
.上式对
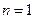 时也成立.
时也成立.以下同解法二,可得
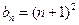 ,
,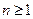 .
.(Ⅲ)证明:
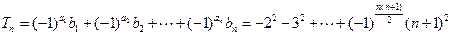 .
.当
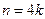 ,
,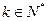 时,
时,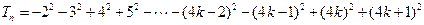 .
.注意到
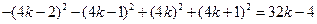 ,故
,故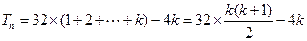
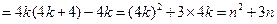 .
.当
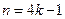 ,
,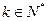 时,
时,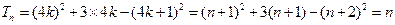
当
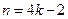 ,
,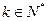 时,
时,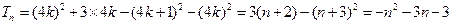 .
.当
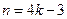 ,
,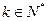 时,
时,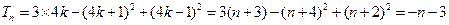 .
.所以
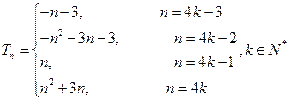 .
.从而
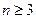 时,有
时,有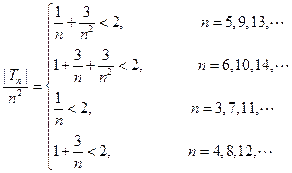
总之,当
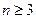 时有
时有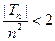 ,即
,即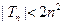 .
.
练习册系列答案
相关题目
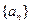 为等差数列,
为等差数列,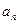 为正整数,其前
为正整数,其前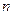 项和为
项和为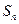 ,数列
,数列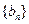 为等比数列,且
为等比数列,且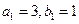 ,数列
,数列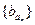 是公比为64的等比数列,
是公比为64的等比数列,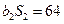 。
。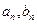 ;
;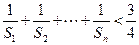 。
。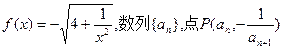 在曲线
在曲线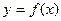 上(
上(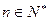 ),且
),且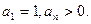
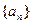 的通项公式;
的通项公式;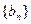 的前n项和为Tn,且满足
的前n项和为Tn,且满足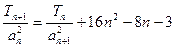 ,试确定b1的值,使得
,试确定b1的值,使得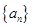 的中,公差
的中,公差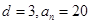 ,前
,前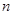 项和
项和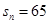 ,则
,则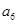 分别为
分别为 
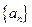 为等比数列,
为等比数列,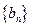 为等差数列,且
为等差数列,且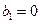 ,
,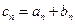 ,若数列
,若数列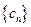 是1,1,2,…,则数列
是1,1,2,…,则数列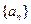 的前
的前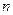 项和为
项和为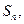 且
且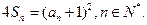
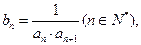 求数列
求数列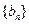 的前
的前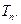
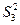 =9S2,
=9S2,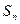 为等差数列
为等差数列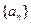 的前
的前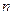 项和,若
项和,若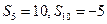 ,则数列
,则数列