题目内容
 如图,棱柱ABCD-A1B1C1D1的所有棱长都为2,AC∩BD=O,则棱AA1与底面ABCD所成的角为60°,A1O⊥平面ABCD,F为DC1的中点.
如图,棱柱ABCD-A1B1C1D1的所有棱长都为2,AC∩BD=O,则棱AA1与底面ABCD所成的角为60°,A1O⊥平面ABCD,F为DC1的中点.(1)证明:BD⊥AA1;
(2)证明:OF∥平面BCC1B1;
(3)求二面角D-AA1-C的余弦值.
分析:(1)先证出BD与面A1ACC1内的两条相交直线AC,AA1垂直,从而证得BD⊥平面A1ACC1,∴BD⊥AA1
(2)先证出OF∥BC1,再由线面平行的判定定理可证OF∥平面BCC1B1
(3)以O为坐标系的原点,分别以OA,OB,OA1所在直线为x,y,z轴建立空间直角坐标系,求出平面AA1D的法向量,平面A1ACC1的法向量,通过两法向量的夹角去解.
(2)先证出OF∥BC1,再由线面平行的判定定理可证OF∥平面BCC1B1
(3)以O为坐标系的原点,分别以OA,OB,OA1所在直线为x,y,z轴建立空间直角坐标系,求出平面AA1D的法向量,平面A1ACC1的法向量,通过两法向量的夹角去解.
解答: 解(1)因为棱柱ABCD-A1B1C1D1的所有棱长都为2,
解(1)因为棱柱ABCD-A1B1C1D1的所有棱长都为2,
所以四边形ABCD为菱形,BD⊥AC
又A1O⊥平面ABCD,BD?平面ABCD,
所以A1O⊥BD.
又因为AC∩A1O=O,AC,A1O?平面A1ACC1,
所以BD⊥平面A1ACC1,
因为AA1?平面A1ACC1
所以BD⊥AA1
(2)连接BC1,因为四边形ABCD为菱形,AC∩BD=O,
所以O是BD的中点
又因为点F为DC1的中点,
所以在△DBC1中,OF∥BC1,
因为OF?平面BCC1B1,BC1?平面BCC1B1,
所以OF∥平面BCC1B1
(3)以O为坐标系的原点,分别以OA,OB,OA1所在直线为x,y,z轴建立空间直角坐标系.因为侧棱AA1与底面ABCD所成角为60°,A1O⊥平面ABCD.
所以∠A1AO=60°,在Rt△A1AO中,可得AO=1,A1O=
,
在Rt△AOB中,OB=
=
=
.A(1,0,0),A1(0,0,
),D(0,-
,0),B(0,
,0)
设平面AA1D的法向量为
=(x1,y1,z1).
•
=0
所以
•
=0
因为
=(-1,0,
),
=(-1,-
,0).
-x1+
z1=0∴-x1-
y1=0,
可设
=(
,-1,1),
又因为BD⊥平面A1ACC1,所以平面A1ACC1的法向量为
=
=(0,
,0),∴cos?
,
>=
=
=-
因为二面角D-AA1-C为锐角,
故二面角D-AA1-C的余弦值是
.
 解(1)因为棱柱ABCD-A1B1C1D1的所有棱长都为2,
解(1)因为棱柱ABCD-A1B1C1D1的所有棱长都为2,所以四边形ABCD为菱形,BD⊥AC
又A1O⊥平面ABCD,BD?平面ABCD,
所以A1O⊥BD.
又因为AC∩A1O=O,AC,A1O?平面A1ACC1,
所以BD⊥平面A1ACC1,
因为AA1?平面A1ACC1
所以BD⊥AA1
(2)连接BC1,因为四边形ABCD为菱形,AC∩BD=O,
所以O是BD的中点
又因为点F为DC1的中点,
所以在△DBC1中,OF∥BC1,
因为OF?平面BCC1B1,BC1?平面BCC1B1,
所以OF∥平面BCC1B1
(3)以O为坐标系的原点,分别以OA,OB,OA1所在直线为x,y,z轴建立空间直角坐标系.因为侧棱AA1与底面ABCD所成角为60°,A1O⊥平面ABCD.
所以∠A1AO=60°,在Rt△A1AO中,可得AO=1,A1O=
| 3 |
在Rt△AOB中,OB=
| AB2-AO2 |
| 4-1 |
| 3 |
| 3 |
| 3 |
| 3 |
设平面AA1D的法向量为
| n1 |
| n1 |
| AA1 |
所以
| n |
| AD |
因为
| AA1 |
| 3 |
| AD |
| 3 |
-x1+
| 3 |
| 3 |
可设
| n |
| 3 |
又因为BD⊥平面A1ACC1,所以平面A1ACC1的法向量为
| n2 |
| OB |
| 3 |
| n1 |
| n2 |
| ||||
|
-
| ||||
|
| ||
| 5 |
因为二面角D-AA1-C为锐角,
故二面角D-AA1-C的余弦值是
| ||
| 5 |
点评:本题考查直线和直线,直线和平面位置关系及其判定,二面角求解,考查转化的思想方法(空间问题平面化)空间想象能力,计算能力.利用空间向量的知识,则使问题论证变成了代数运算,使人们解决问题更加方便.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
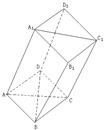 如图,棱柱ABCD-A1B1C1D1的所有棱长都等于2,∠ABC和∠A1B1C1均为60°,平面AA1C1C⊥平面ABCD.
如图,棱柱ABCD-A1B1C1D1的所有棱长都等于2,∠ABC和∠A1B1C1均为60°,平面AA1C1C⊥平面ABCD. 如图四棱柱ABCD-A1B1C1D1的底面ABCD为正方形,侧棱与底边长均为a,且∠A1AD=∠A1AB=60°.
如图四棱柱ABCD-A1B1C1D1的底面ABCD为正方形,侧棱与底边长均为a,且∠A1AD=∠A1AB=60°.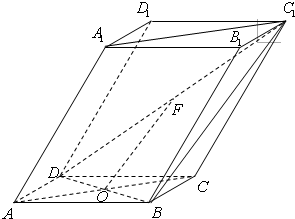 17、如图,棱柱ABCD-A1B1C1D1的底面ABCD为菱形,AC∩BD=O,侧棱AA1⊥BD,点F为DC1的中点.
17、如图,棱柱ABCD-A1B1C1D1的底面ABCD为菱形,AC∩BD=O,侧棱AA1⊥BD,点F为DC1的中点.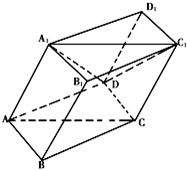 如图,棱柱ABCD-A1B1C1D1的底面ABCD为菱形,平面AA1C1C⊥平面ABCD.?
如图,棱柱ABCD-A1B1C1D1的底面ABCD为菱形,平面AA1C1C⊥平面ABCD.?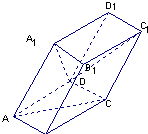 如图,棱柱ABCD-A1B1C1D1的所有棱长都等于2,∠ABC=60°,平面AA1CC1⊥平面ABCD,∠A1AC=60°
如图,棱柱ABCD-A1B1C1D1的所有棱长都等于2,∠ABC=60°,平面AA1CC1⊥平面ABCD,∠A1AC=60°