Question

如图，在直三棱柱ABC­A₁B₁C₁中，AB＝BC＝2AA₁，∠ABC＝90°，D是BC的中点．

(1)求证：A₁B∥平面ADC₁；

(2)求二面角C₁­AD­C的余弦值；

(3)试问线段A₁B₁上是否存在一点E，使AE与DC₁成60°角？若存在，确定E点位置；若不存在，说明理由．

Answer 1

解：(1)连接A₁C，交AC₁于点O，连接OD.

由ABC­A₁B₁C₁是直三棱柱，得四边形ACC₁A₁为矩形，O为A₁C的中点．

又D为BC的中点，所以OD为△A₁BC的中位线，

所以A₁B∥OD，

因为OD⊂平面ADC₁，A₁B⊄平面ADC₁，

所以A₁B∥平面ADC₁.

(2)由ABC­A₁B₁C₁是直三棱柱，且∠ABC＝90°，得BA、BC、BB₁两两垂直．以B为坐标原点，以BC、BA、BB₁所在直线分别为x、y、z轴，建立如图所示的空间直角坐标系B­xyz.

设BA＝2，则B(0，0，0)，C(2，0，0)，A(0，2，0)，C₁(2，0，1)，D(1，0，0)，

所以＝(1，－2，0)，＝(2，－2，1)

设平面ADC₁的法向量为n＝(x，y，z)，

则有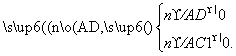

所以取y＝1，得n＝(2，1，－2)．

易知平面ADC的一个法向量为v＝(0，0，1)．

所以cos 〈n，v〉＝＝－.

因为二面角C₁­AD­C是锐二面角，

所以二面角C₁­AD­C的余弦值为.

(3)假设存在满足条件的点E.

因为点E在线段A₁B₁上，A₁(0，2，1)，B₁(0，0，1)，故可设E(0，λ，1)，其中0≤λ≤2.

所以＝(0，λ－2，1)，＝(1，0，1)．

因为AE与DC₁成60°角，所以

|cos 〈，〉|＝|＝.

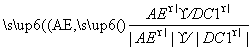即||＝，解得λ＝1或λ＝3(舍去)．

所以当点E为线段A₁B₁的中点时，AE与DC₁成60°角．

                            

可得,   所以                      

从而有,,                   

由,得     

此时.                  

当且仅当,时,成等比数列