题目内容
定义全集U的子集A的特征函数为fA(x)=
,这里CUA表示A在全集U中的补集,那么对于集合A、B⊆U,下列所有正确说法的序号是
(1)A⊆B⇒fA(x)≤fB(x) (2)fCUA(x)=1-fA(x)
(3)fA∩B(x)=fA(x)•fB(x) (4)fA∪B(x)=fA(x)+fB(x)
|
(1),(2),(3)
(1),(2),(3)
. (1)A⊆B⇒fA(x)≤fB(x) (2)fCUA(x)=1-fA(x)
(3)fA∩B(x)=fA(x)•fB(x) (4)fA∪B(x)=fA(x)+fB(x)
分析:利用特征函数的定义知:(1)由A⊆B,对x与A、B关系分类讨论,可得(1)正确;(2)fCUA(x)=
=1-fA(x);(3)fA∩B(x)=
=
=fA(x)•fB(x);(4)fA∪B(x)=
≠fA(x)+fB(x).
|
|
|
|
解答:解:由fA(x)=
,知:
(1)∵A⊆B,分类讨论:
①当x∈A,则x∈B,此时fA(x)=fB(x)=1,
②当x∉A,且x∉B,即x∈?uB此时fA(x)=fB(x)=0,
③当x∉A,且x∈B,即x∈(?uA)∩B时,fA(x)=0,fB(x)=1,此时fA(x)≤fB(x),
综合有fA(x)≤fB(x),故(1)正确;
(2)fCUA(x)=
=1-fA(x),故(2)正确;
(3)fA∩B(x)=
=
=
•
=fA(x)•fB(x),故(3)成立;
(4)fA∪B(x)=
≠fA(x)+fB(x),故(4)不成立.
故答案为:(1),(2),(3).
|
(1)∵A⊆B,分类讨论:
①当x∈A,则x∈B,此时fA(x)=fB(x)=1,
②当x∉A,且x∉B,即x∈?uB此时fA(x)=fB(x)=0,
③当x∉A,且x∈B,即x∈(?uA)∩B时,fA(x)=0,fB(x)=1,此时fA(x)≤fB(x),
综合有fA(x)≤fB(x),故(1)正确;
(2)fCUA(x)=
|
(3)fA∩B(x)=
|
=
|
=
|
|
=fA(x)•fB(x),故(3)成立;
(4)fA∪B(x)=
|
故答案为:(1),(2),(3).
点评:本题考查子集与交集、并集运算的转换及应用,解题时要认真审题,注意特征函数的定义的灵活运用.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
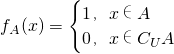 ,这里CUA表示A在全集U中的补集,那么对于集合A、B⊆U,下列所有正确说法的序号是______.
,这里CUA表示A在全集U中的补集,那么对于集合A、B⊆U,下列所有正确说法的序号是______. 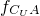 (x)=1-fA(x)
(x)=1-fA(x)