题目内容
本小题满分10分
已知二次函数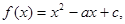 (其中
(其中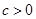 ).
).
(1)若函数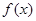 为偶函数,求
为偶函数,求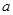 的值;
的值;
(2)当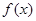 为偶函数时,若函数
为偶函数时,若函数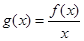 ,指出
,指出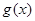 在
在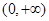 上单调性情况,并证明之.
上单调性情况,并证明之.
已知二次函数
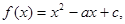 (其中
(其中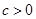 ).
).(1)若函数
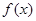 为偶函数,求
为偶函数,求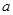 的值;
的值;(2)当
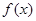 为偶函数时,若函数
为偶函数时,若函数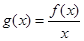 ,指出
,指出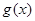 在
在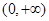 上单调性情况,并证明之.
上单调性情况,并证明之.(1) ;(2)见解析。
;(2)见解析。
 ;(2)见解析。
;(2)见解析。本试题主要是考查了二次函数的奇偶性和函数的单调性的运用。
(1)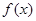 为偶函数,即对任意
为偶函数,即对任意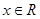 ,
,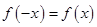
即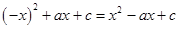 ,即
,即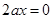 对任意
对任意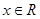 恒成立,得到a的值为零。
恒成立,得到a的值为零。
(2)由(1),若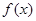 为偶函数,则
为偶函数,则 ,
,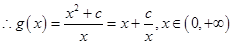
当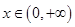 时,
时,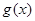 在
在 上单调递减,在
上单调递减,在 上单调递增,然后结合定义法证明。
上单调递增,然后结合定义法证明。
解:(1)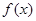 为偶函数,即对任意
为偶函数,即对任意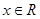 ,
,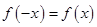 ……………2分
……………2分
即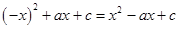 ,即
,即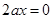 对任意
对任意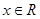 恒成立 ……………3分
恒成立 ……………3分
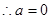 ……………4分
……………4分
(2)由(1),若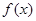 为偶函数,则
为偶函数,则 ,
,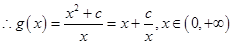
当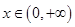 时,
时,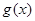 在
在 上单调递减,在
上单调递减,在 上单调递增,证明如下: ……………5分
上单调递增,证明如下: ……………5分
设任意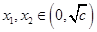 ,且
,且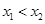
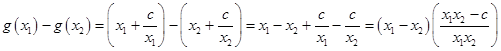 ……………7分
……………7分
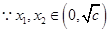 ,且
,且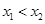 ,
,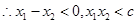 ,即
,即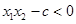
 ,即
,即 即
即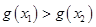

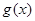 在
在 上单调递减 ……………9分
上单调递减 ……………9分
同理,可得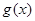 在
在 上单调递增 ……………10分
上单调递增 ……………10分
(1)
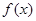 为偶函数,即对任意
为偶函数,即对任意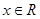 ,
,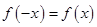
即
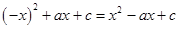 ,即
,即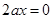 对任意
对任意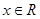 恒成立,得到a的值为零。
恒成立,得到a的值为零。(2)由(1),若
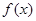 为偶函数,则
为偶函数,则 ,
,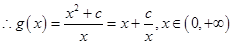
当
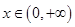 时,
时,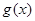 在
在 上单调递减,在
上单调递减,在 上单调递增,然后结合定义法证明。
上单调递增,然后结合定义法证明。解:(1)
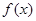 为偶函数,即对任意
为偶函数,即对任意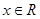 ,
,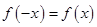 ……………2分
……………2分即
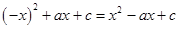 ,即
,即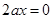 对任意
对任意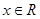 恒成立 ……………3分
恒成立 ……………3分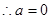 ……………4分
……………4分(2)由(1),若
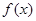 为偶函数,则
为偶函数,则 ,
,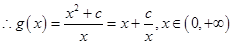
当
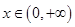 时,
时,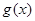 在
在 上单调递减,在
上单调递减,在 上单调递增,证明如下: ……………5分
上单调递增,证明如下: ……………5分设任意
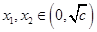 ,且
,且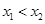
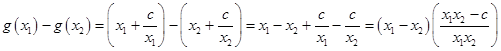 ……………7分
……………7分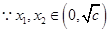 ,且
,且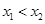 ,
,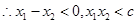 ,即
,即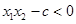
 ,即
,即 即
即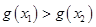

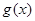 在
在 上单调递减 ……………9分
上单调递减 ……………9分同理,可得
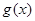 在
在 上单调递增 ……………10分
上单调递增 ……………10分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
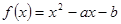 的两个零点是2和3,则函数
的两个零点是2和3,则函数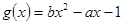 的零点是( )
的零点是( ) 和
和
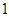 和
和
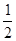 和
和
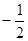 和
和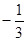
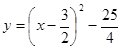 的定义域为[0 , m],值域为
的定义域为[0 , m],值域为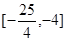 ,则m的取值范围是( )
,则m的取值范围是( )

 )
)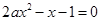 在(0,1)内恰有一解,则
在(0,1)内恰有一解,则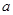 的取值范围是
的取值范围是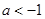
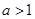
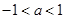
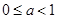
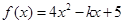 ,当
,当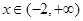 时是增函数,当
时是增函数,当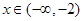 时是减函数,则
时是减函数,则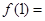 _________
_________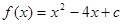 ,求
,求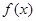 的单调递减区间。
的单调递减区间。 在区间
在区间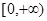 上单调递减,求实数
上单调递减,求实数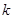 的取值范围。
的取值范围。