题目内容
3.在△ABC中,角A、B、C所对的边分别是a,b,c,若bsinA=3csinB,a=3,$cosB=\frac{2}{3}$,则b的值为$\sqrt{6}$.分析 利用正弦定理化简已知等式,根据b不为0得到a=3c,把a的值代入求出c的值,利用余弦定理表示出cosB,将各自的值代入即可求出b的值.
解答 解:利用正弦定理化简bsinA=3csinB,得:ab=3bc,
∵b≠0,∴a=3c,
把a=3代入得:c=1,
由余弦定理得:cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$=$\frac{9+1-{b}^{2}}{6}$=$\frac{2}{3}$,
解得:b=$\sqrt{6}$.
故答案为:$\sqrt{6}$
点评 此题考查了正弦、余弦定理,熟练掌握正弦、余弦定理是解本题的关键.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
13.直线y=ax+b通过第一、二、三象限,则圆(x+a)2+(y+b)2=r2(r>0)的圆心位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |




 ,若
,若 是从
是从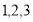 三个数中任取的一个数,
三个数中任取的一个数, 是从
是从 三个数中任取的一个数,则使函数
三个数中任取的一个数,则使函数 有极值点的概率为_______.
有极值点的概率为_______. 中,曲线
中,曲线 的参数方程为
的参数方程为 (
( 为参数,
为参数,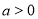 ),在以坐标原点为极点,
),在以坐标原点为极点, 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线 .
. 的极坐标方程为
的极坐标方程为 ,其中
,其中 满足
满足 ,若曲线
,若曲线 的公共点都在
的公共点都在 上,求
上,求 .
.