题目内容
己知数列{an}满足a1,an+1=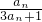 .
.
(I)求数列{an}的通项公式;
(II)记Sn=a1a2+a2a3+…+anan+1,求Sn.
解:(Ⅰ)由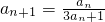 ,得
,得 ,(3分)
,(3分)
∴数列{ }是首项为1,公差为3的等差数列,
}是首项为1,公差为3的等差数列,
∴ ,
,
即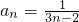 .(6分)
.(6分)
(Ⅱ)∵ =(
=( )×
)× ,(9分)
,(9分)
∴ +…+(
+…+( -
- )]
)]
=
 =
=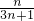 .(12分)
.(12分)
分析:(Ⅰ) 由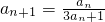 ,得
,得 ,由此能求出数列{an}的通项公式.
,由此能求出数列{an}的通项公式.
(Ⅱ)由 =(
=( )×
)× ,利用裂项求和法能够求出Sn.
,利用裂项求和法能够求出Sn.
点评:本题考查数列的通项公式和前n项和公式的求法,解题时要认真审题,仔细解答,注意合理地进行等价转化.
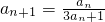 ,得
,得 ,(3分)
,(3分)∴数列{
 }是首项为1,公差为3的等差数列,
}是首项为1,公差为3的等差数列,∴
 ,
,即
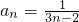 .(6分)
.(6分)(Ⅱ)∵
 =(
=( )×
)× ,(9分)
,(9分)∴
 +…+(
+…+( -
- )]
)]=

 =
=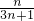 .(12分)
.(12分)分析:(Ⅰ) 由
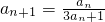 ,得
,得 ,由此能求出数列{an}的通项公式.
,由此能求出数列{an}的通项公式.(Ⅱ)由
 =(
=( )×
)× ,利用裂项求和法能够求出Sn.
,利用裂项求和法能够求出Sn.点评:本题考查数列的通项公式和前n项和公式的求法,解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目