题目内容
已知椭圆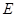 的两个焦点分别为
的两个焦点分别为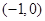 和
和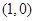 ,离心率
,离心率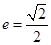 .
.
(1)求椭圆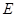 的方程;
的方程;
(2)若直线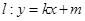 (
(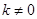 )与椭圆
)与椭圆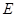 交于不同的两点
交于不同的两点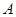 、
、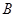 ,且线段
,且线段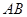
的垂直平分线过定点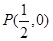 ,求实数
,求实数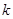 的取值范围.
的取值范围.
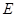 的两个焦点分别为
的两个焦点分别为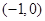 和
和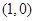 ,离心率
,离心率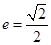 .
.(1)求椭圆
 的方程;
的方程;(2)若直线
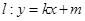 (
(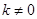 )与椭圆
)与椭圆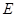 交于不同的两点
交于不同的两点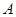 、
、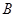 ,且线段
,且线段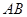
的垂直平分线过定点
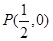 ,求实数
,求实数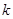 的取值范围.
的取值范围.(1)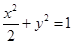 ;(2)
;(2)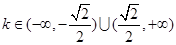 .
.
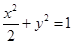 ;(2)
;(2)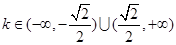 .
.试题分析:(1)求椭圆的标准方程
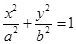 ,要找两个等式以确定
,要找两个等式以确定 ,本题中有焦点为,说明
,本题中有焦点为,说明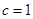 ,又有离心率,即
,又有离心率,即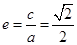 ,由此再加上
,由此再加上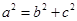 可得结论;(2)直线与圆锥曲线相交问题,又涉及到交点弦,因此我们都是把直线方程(或设出)
可得结论;(2)直线与圆锥曲线相交问题,又涉及到交点弦,因此我们都是把直线方程(或设出)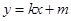 与椭圆方程联立方程组,然后消去
与椭圆方程联立方程组,然后消去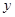 (有时也可消去
(有时也可消去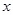 )得关于
)得关于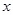 (或
(或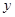 )的一元二次方程,再设交点为
)的一元二次方程,再设交点为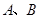 坐标为
坐标为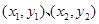 ,则可得
,则可得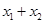 ,
,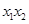 ,(用
,(用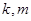 表示),于是
表示),于是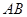 中点
中点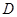 坐标
坐标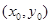 可得,其中
可得,其中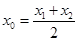 ,
,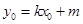 ,而
,而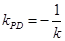 ,从而建立了
,从而建立了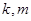 的一个等量关系,在刚才的一元二次方程中,还有判别式
的一个等量关系,在刚才的一元二次方程中,还有判别式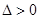 ,合起来可得出关于
,合起来可得出关于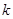 的不等式,从而求出其范围.
的不等式,从而求出其范围.试题解析:(1)由已知椭圆的焦点在
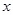 轴上,
轴上,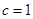 ,
,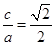 ,
,
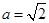 ,
,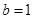 , 2分
, 2分 椭圆
椭圆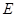 的方程为
的方程为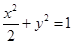 4分
4分(2)
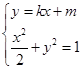 ,消去
,消去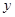 得
得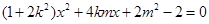 6分
6分 直线
直线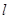 与椭圆有两个交点,
与椭圆有两个交点,
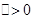 ,可得
,可得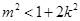 (*) 8分
(*) 8分设
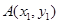 ,
,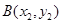

 ,
,
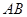 中点的横坐标
中点的横坐标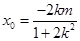
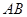 中点的纵坐标
中点的纵坐标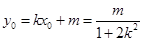 10分
10分
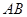 的中点
的中点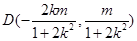
设
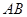 中垂线
中垂线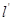 的方程为:
的方程为: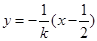
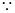
 在
在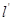 上,
上,
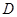 点坐标代入
点坐标代入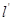 的方程可得
的方程可得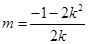 (**) 12分
(**) 12分将
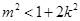 (*)代入解得
(*)代入解得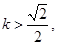 或
或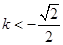 ,
,
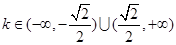 14分
14分
练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
 的左、右焦点分别为
的左、右焦点分别为 ,其上顶点为
,其上顶点为 已知
已知 是边长为
是边长为 的正三角形.
的正三角形.
 的方程;
的方程; 任作一动直线
任作一动直线 交椭圆
交椭圆 两点,记
两点,记 .若在线段
.若在线段 上取一点
上取一点 ,使得
,使得 ,当直线
,当直线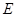 的方程为
的方程为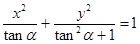 ,其中
,其中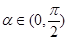 .
.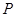 ,证明:点
,证明:点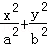 =1(a>b>0)与双曲线C2:x2﹣
=1(a>b>0)与双曲线C2:x2﹣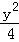 =1有公共的焦点,C2的一条渐近线与以C1的长轴为直径的圆相交于A,B两点.若C1恰好将线段AB三等分,则( )
=1有公共的焦点,C2的一条渐近线与以C1的长轴为直径的圆相交于A,B两点.若C1恰好将线段AB三等分,则( )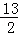

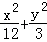 =1的焦点为F1和F2,点P在椭圆上,如果线段PF1的中点在y轴上,那么|PF1|是|PF2|的( )
=1的焦点为F1和F2,点P在椭圆上,如果线段PF1的中点在y轴上,那么|PF1|是|PF2|的( )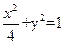 截得的最大弦长等于( )
截得的最大弦长等于( )


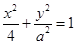 与双曲线
与双曲线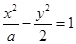 有相同的焦点,则
有相同的焦点,则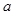 的值是( )
的值是( )

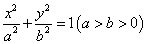 的两个焦点分别为
的两个焦点分别为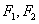 ,点
,点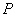 在椭圆上,且
在椭圆上,且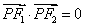 ,
,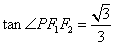 ,则该椭圆的离心率为 .
,则该椭圆的离心率为 .